\begin{frame}
  \frametitle{Aggregations}

  \begin{block}{}
    SQL-92 defines the five main aggregation functions
    \begin{tcenter}
      \sql{count}, \sql{sum}, \sql{avg}, \sql{max}, \sql{min}
    \end{tcenter}
  \end{block}

  Some DBMS define more functions:
  \begin{tcenter}
    \sql{correlation}, \sql{stddev}, \sql{variance}, \dots 
  \end{tcenter}
  \pause\medskip

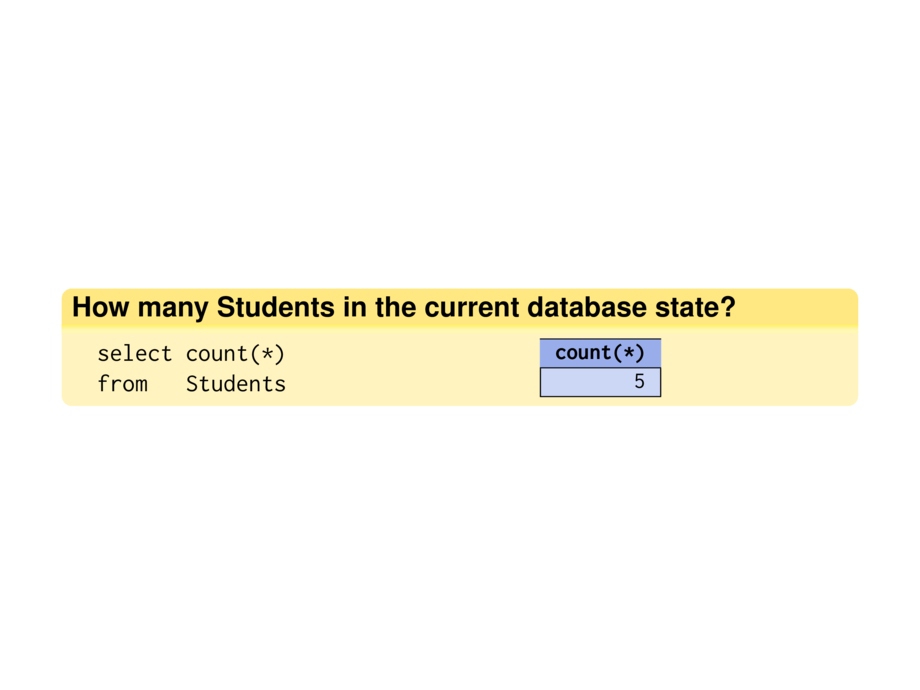
  \countStudents
  \pause
  
  \begin{goal}{}
    Some aggregation functions are sensitive to \emph{duplicates}:
    \begin{tcenter}
      \sql{sum}, \sql{count}, \sql{avg}\;,
    \end{tcenter}
    some are insensitive:
    \begin{tcenter}
      \sql{min}, \sql{max}
    \end{tcenter}
  \end{goal}
  SQL allows to explicitly request to ignore duplicates, e.g.:
    \begin{tcenter}
      $\cdots$ \sql{count(distinct A)} $\cdots$
    \end{tcenter}

    %   \item Any \emph{commutative} and \emph{associative} binary
    %     operator with a neutral element can be extended (``\emph{lifted}'')
    %     to work on set-valued arguments (\emph{e.g.}, \sql{sum} corresponds
    %     to \sql{+}).
    %   \end{itemize}
    %
    %   \begin{quiz}{\textwidth}{Commutative and associative, neutral element?}
    %     Why do we require these properties of the operators?
    %   \end{quiz}
\end{frame}