\begin{frame}
  \frametitle{Examples}

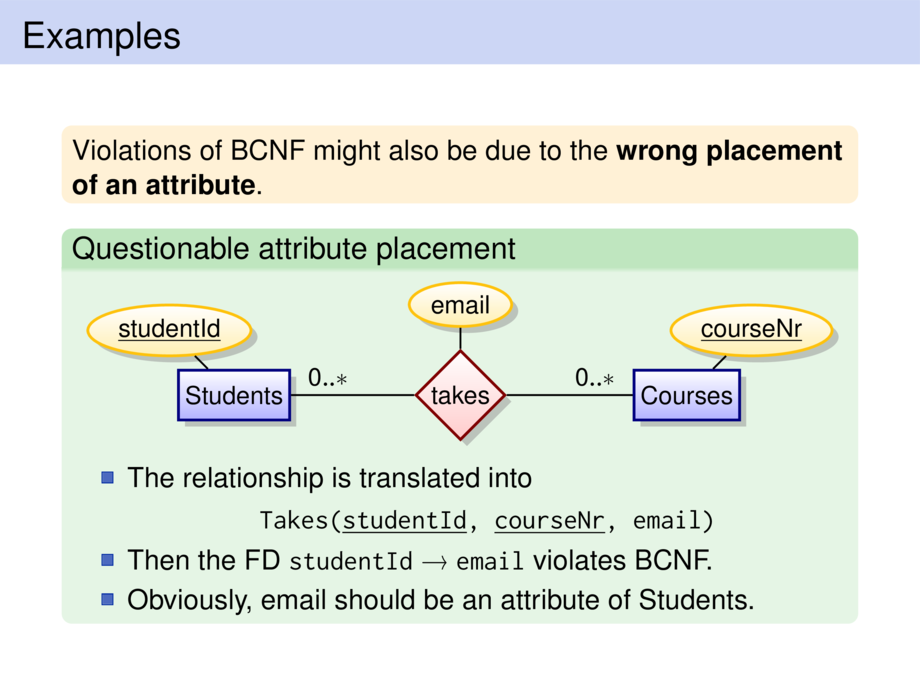
  \begin{goal}{}
    If an attribute of a ternary relationship depends only on two of
    the entities, this violates BCNF.
  \end{goal}

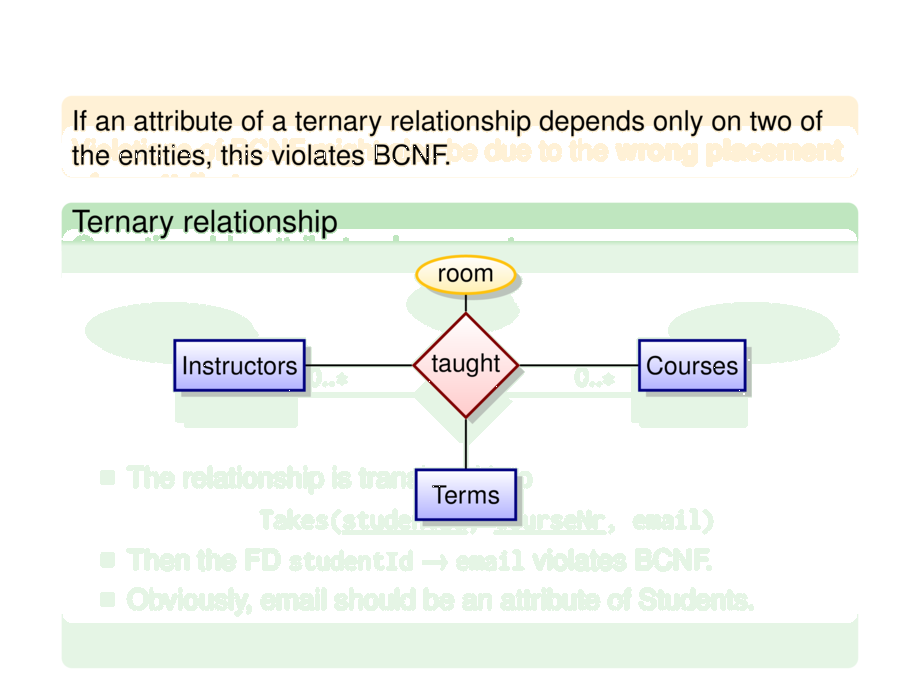
  \begin{exampleblock}{Ternary relationship}
    \begin{tcenter}
      \scalebox{.9}{
      \begin{tikzpicture}[every edge/.style={link}]
        \node[entity] (instructor) {Instructors};
        \node[entity,xshift=70mm] (course) {Courses};
        \node[entity,xshift=35mm,yshift=-20mm] (term) {Terms};
        
        \node[relationship] at($(instructor)!.5!(course)$) (taught) {taught}
          edge (instructor)
          edge (course)
          edge (term);

        \node[attribute] [at=(taught),shift={(0cm,1.4cm)}] {room} edge (taught);
      \end{tikzpicture}
      }
    \end{tcenter}
    \pause
    \medskip
    
    If every course is taught only once per term, then attribute
    room depends only on term and course (but not instructor).
    \pause
    \medskip
    
    Then the FD $\sql{term},\sql{course} \to \sql{room}$ violates BCNF.
  \end{exampleblock}
\end{frame}