




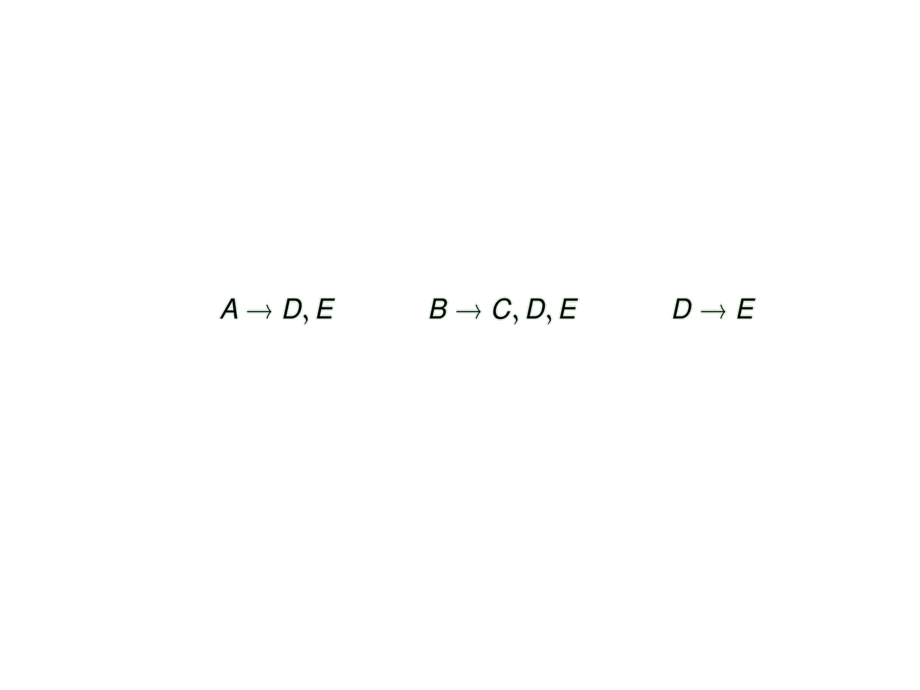






























































































217/291
\begin{frame}
\frametitle{BCNF Synthesis Algorithm: Example}
\begin{exampleblock}{}
Consider $R = (A,B,C,D,E)$ with the canonical set of FDs
\begin{talign}
A \to D &&
B \to C &&
B \to D &&
D \to E
\end{talign}
Here $\{\,A,B\,\}$ is the only minimal key. \pause Is $R$ in BCNF? \pause No.
\begin{enumerate}
\pause
\item Maximise the right-hand sides of the FDs:
\pause
\begin{talign}
A \to D,E &&
B \to C,D,E &&
D \to E
\end{talign}
\item \pause Split off violating FD's one by one:
\begin{itemize}
\pause
\item $\mathcal{S} = \{\, R_0(\ul{A},\ul{B},C,D,E) \,\}$
\pause
\item $A \to D,E$ violates BCNF of $R_0$
\pause
\item $\mathcal{S} = \{\, R_0(\ul{A},\ul{B},C),\; R_1(\ul{A},D,E) \,\}$
\pause
\item $B \to C,D,E$ violates BCNF of $R_0$
\pause
\item $\mathcal{S} = \{\, R_0(\ul{A},\ul{B}),\; R_1(\ul{A},D,E),\; R_2(\ul{B},C) \,\}$
\pause
\item $D \to E$ violates BCNF of $R_1$
\pause
\item $\mathcal{S} = \{\, R_0(\ul{A},\ul{B}),\; R_1(\ul{A},D),\; R_2(\ul{B},C),\; R_3(\ul{D},E) \,\}$\pause\ - done!
\end{itemize}
\end{enumerate}
\end{exampleblock}
Note that we lost the dependency $B \to D$!
\end{frame}

