


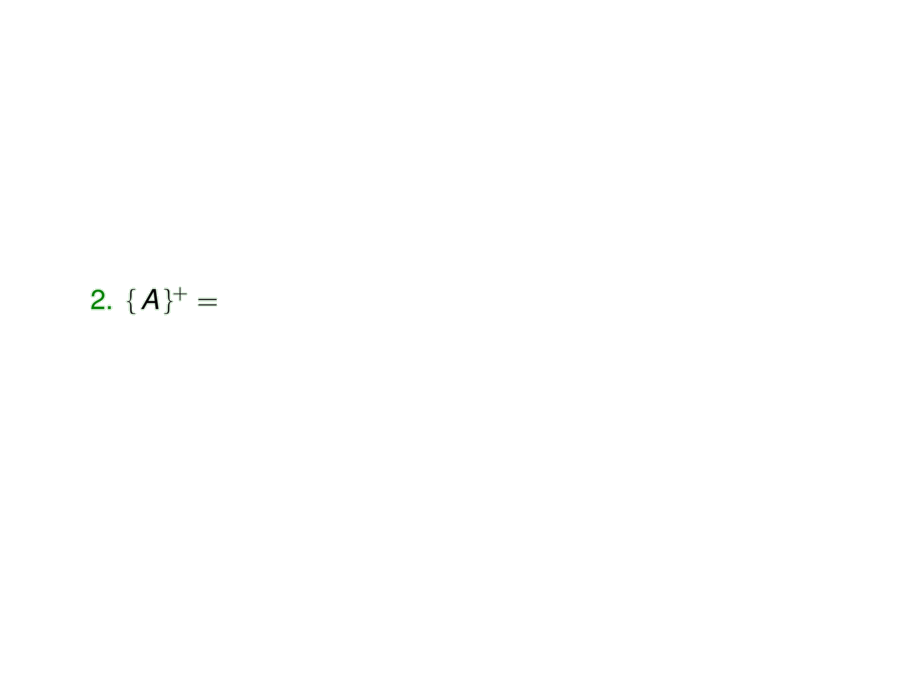
































































































130/291
\begin{frame}
\frametitle{How to Determine Keys: Examples}
\begin{exampleblock}{}
Find \emph{all} minimal keys the relation $\sql{R(A,B,C,D,E)}$ with
\begin{talign}
A, D &\to B, D &
B, D &\to C &
A &\to E
\end{talign}
We get
\begin{enumerate}
\pause
\item $\textit{Candidates} = \{\; \{\, A \,\} \;\}$ since $A$ not in any right-hand side
\pause
\item $\{\, A \,\}^+ = \pause \{\, A,E \,\}$\pause, so we extend with $B,C,D$:
$\textit{Candidates} = \{\; \{\, A,B \,\}, \{\, A,C \,\}, \{\, A,D \,\} \;\}$
\pause
\item $\{\, A,D \,\}^+ = \pause \{\, A,B,C,D,E \,\}$. So $\{\, A,D \,\}$ is a \emph{key}.
\pause
\item $\{\, A,B \,\}^+ = \pause \{\, A,B,E \,\}$\pause, so we extend with $C,D$:
$\textit{Candidates} = \{\; \{\, A,B,C \,\}, \{\, A,B,D \,\}, \{\, A,C \,\} \;\}$
\pause
\item $\{\, A,C \,\}^+ = \pause \{\, A,C,E \,\}$\pause, so we extend with $B,D$:
$\textit{Candidates} = \{\; \{\, A,B,C \,\}, \{\, A,B,D \,\}, \{\, A,C,D \,\} \;\}$
\pause
\item Remove $\{\, A,B,D \,\}$ and $\{\, A,C,D \,\}$ since they contain a key.
\pause
\item $\{\, A,B,C \,\}^+ = \{\, A,B,C,E \,\}$ is not a key!\\
Extension with $D$ again contains a key.
\end{enumerate}
\end{exampleblock}
\end{frame}

