


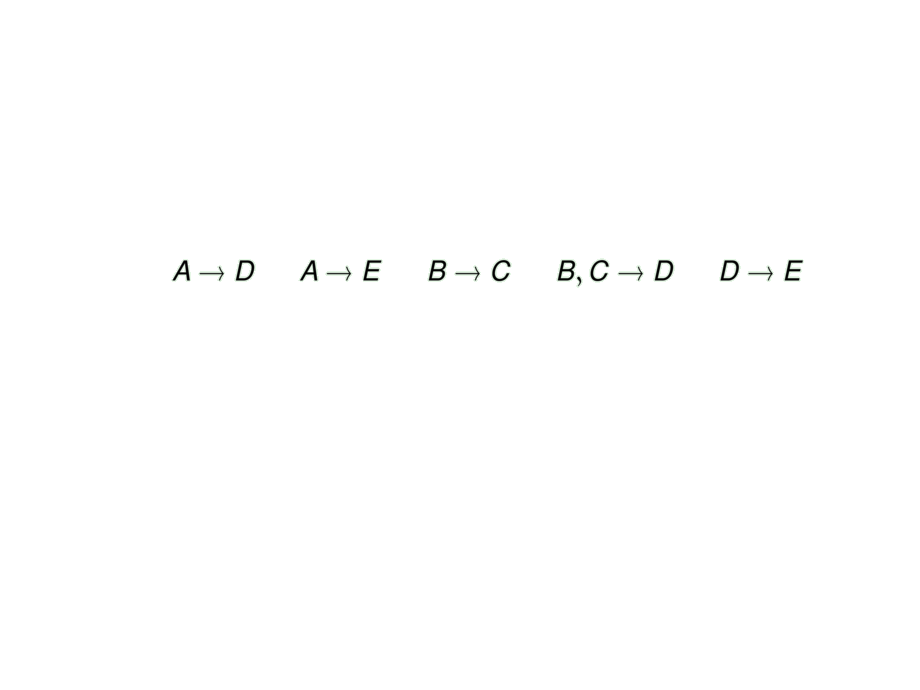
































































































97/291
\begin{frame}
\frametitle{Canonical Set of Functional Dependencies}
\begin{exampleblock}{}
Consider the relation $R(A,B,C,D,E)$ with FDs
\begin{talign}
A \to D,E && B \to C && B,C \to D && D \to E
\end{talign}\vspace{-2ex}
\begin{enumerate}
\pause
\item
Make the right-hand sides singular\pause
\begin{talign}
A \to D && A \to E && B \to C && B,C \to D && D \to E
\end{talign}\vspace{-3ex}
\pause
\item
Minimise left-hand sides\pause
\begin{talign}
A \to D && A \to E && B \to C && B \to D && D \to E
\end{talign}
We drop $C$ from $B,C \to D$ since $D \in \{\,B\,\}^+$ due to $B \to C$.
\pause
\item Remove implied FDs\pause
\begin{talign}
A \to D && B \to C && B \to D && D \to E
\end{talign}
$A \to E$ can still be derived from $A \to D$ and $D \to E$.
\end{enumerate}
\pause\smallskip
Thus we have obtained the following \emph{canonical} set of FDs:
\begin{talign}
A \to D && B \to C && B \to D && D \to E
\end{talign}
\end{exampleblock}
\end{frame}

