\begin{frame}
  \frametitle{Relationship Sets with Attributes}

  \begin{goal}{}
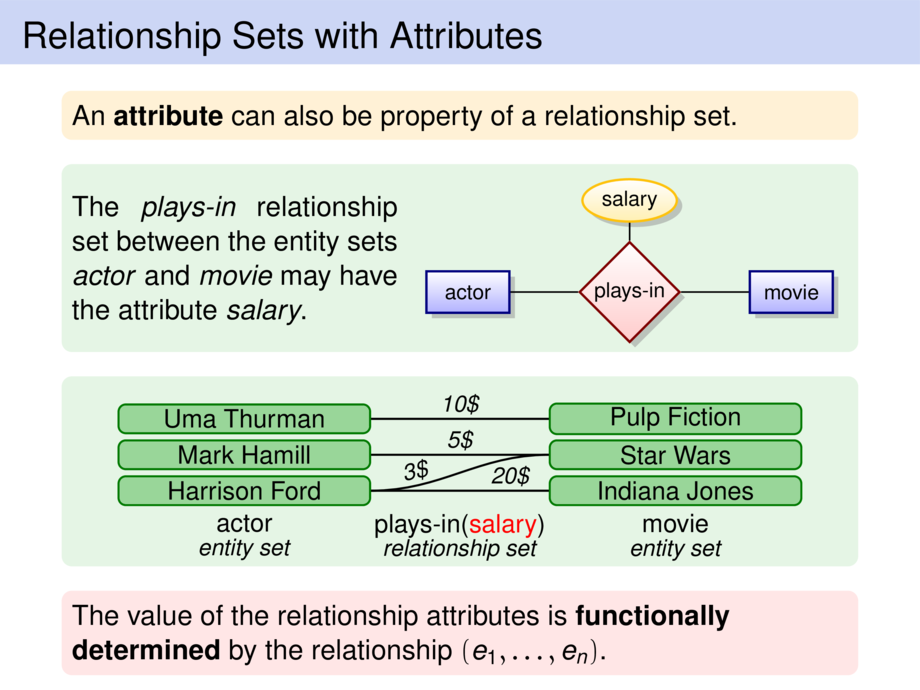
  An \emph{attribute} can also be property of a relationship set.
  \end{goal}
  
  \begin{exampleblock}{}
    \begin{minipage}{.42\textwidth}
    The \textit{plays-in} relationship set between the
    entity~sets \textit{actor} and \textit{movie} may have the attribute \textit{salary}.
    \end{minipage}
    \begin{minipage}{.57\textwidth}
    \begin{center}
      \scalebox{.75}{
      \begin{tikzpicture}[every edge/.style={link}]
        \node[entity] (actor) {actor};
        \node[entity,right of=actor, node distance=6cm] (movie) {movie};

        \node[relationship] (plays) at ($(actor)!.5!(movie)$) {plays-in} edge (actor) edge (movie);
        \node[attribute] (id) [above of=plays,node distance=1.7cm] {salary} edge (plays);
      \end{tikzpicture}}
    \end{center}
    \end{minipage}
  \end{exampleblock}
  \pause

  \begin{exampleblock}{}
    \begin{center}
      {\small
      \begin{tikzpicture}[default,node distance=5mm]
        \begin{scope}[nodes={rectangle, draw=cgreen!80!black, minimum width=35mm, minimum height=4mm, rounded corners=1mm, fill=cgreen!40}]
        \node (a1) {Uma Thurman};
        \node (a2) [below of=a1] {Mark Hamill};
        \node (a3) [below of=a2] {Harrison Ford};

        \node (s1) [right of=a1,node distance=60mm] {Pulp Fiction};
        \node (s2) [below of=s1] {Star Wars};
        \node (s3) [below of=s2] {Indiana Jones};
        \end{scope}
        \begin{scope}[node distance=7mm]
        \node (l) [below of=a3,align=center] {actor\\[-.5ex] \remark{entity set}};
        \node (r) [below of=s3,align=center] {movie\\[-.5ex] \remark{entity set}};
        \node at ($(l)!.5!(r)$) [align=center] {plays-in(\alert{salary})\\[-.5ex]\remark{relationship set}};
        \end{scope}
        \draw (a1) to[out=0,in=180] node [sloped,above] {\remark{10\$}} (s1);
        \draw (a2) to[out=0,in=180] node [sloped,above] {\remark{5\$}} (s2);
        \draw (a3) to[out=0,in=180]  node [sloped,above,pos=.25] {\remark{3\$}} (s2);
        \draw (a3) to[out=0,in=180]  node [sloped,above,pos=.8] {\remark{20\$}} (s3);
      \end{tikzpicture}}\vspace{-1ex}
    \end{center}
  \end{exampleblock}
  \pause
  
  \begin{alertblock}{}
    The value of the relationship attributes is \emph{functionally determined} 
    by the relationship $(e_1,\ldots,e_n)$.
  \end{alertblock}
\end{frame}