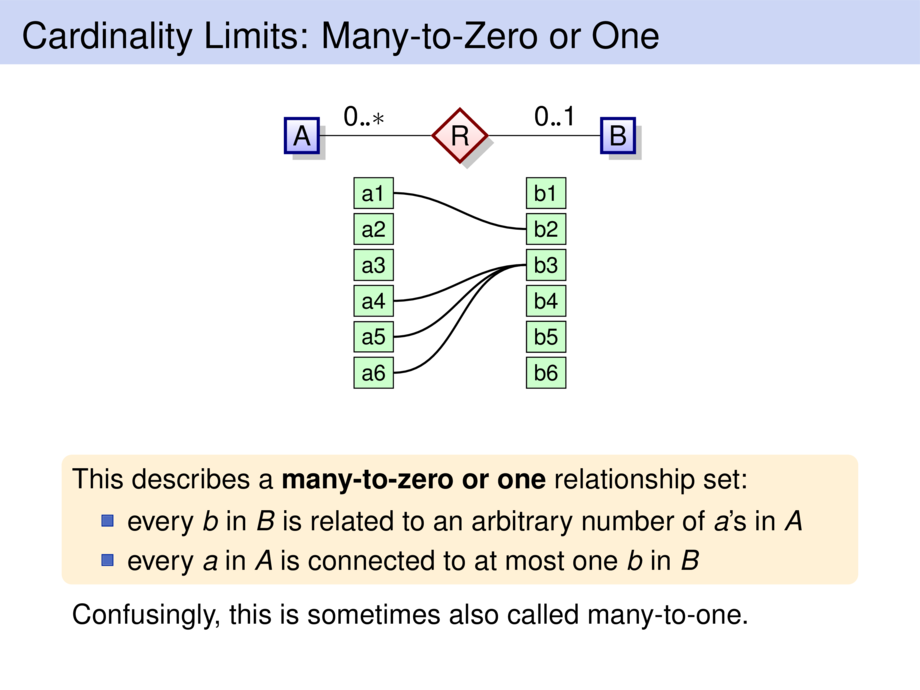
































































































34/98
\begin{frame}
\frametitle{Express the following Cardinality Limits}
\begin{quiz}{\textwidth}{}
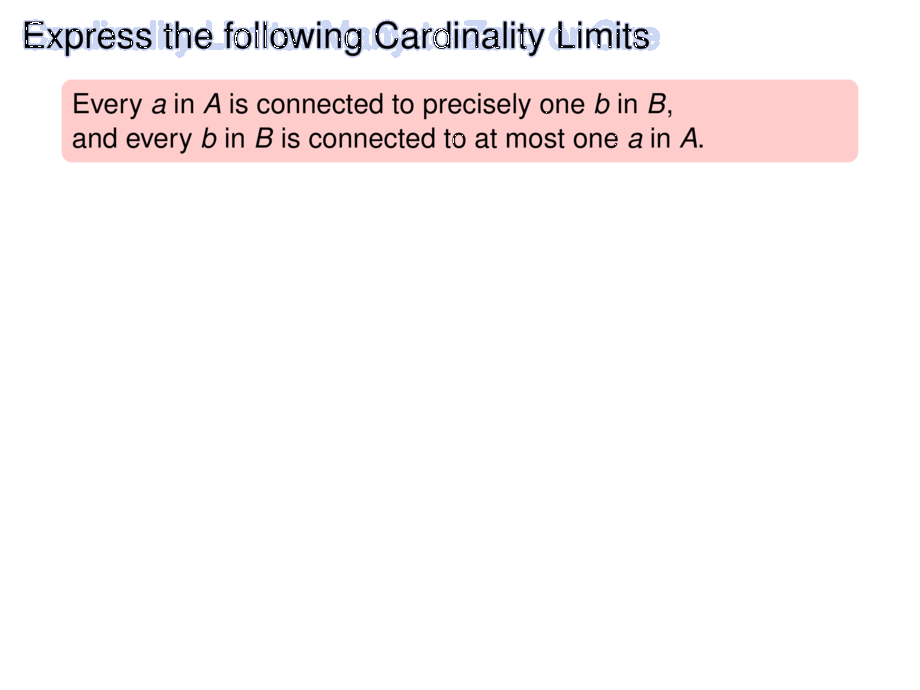
Every $a$ in $A$ is connected to precisely one $b$ in $B$,\\
and every $b$ in $B$ is connected to at most one $a$ in $A$.
\end{quiz}
\pause
\begin{center}
\begin{tikzpicture}[every edge/.style={link},node distance=18mm,>=triangle 45]
\begin{scope}
\node[relationship] (R) {R};
\node (l) [left of=R,entity,minimum size=4mm] {A}; \draw (R) -- node[above,pos=.6] {$0\sldots1$} (l);
\node (r) [right of=R,entity,minimum size=4mm] {B}; \draw (R) -- node[above,pos=.7] {$1\sldots 1$} (r);
\end{scope}
\end{tikzpicture}
\end{center}
\pause
\begin{quiz}{\textwidth}{}
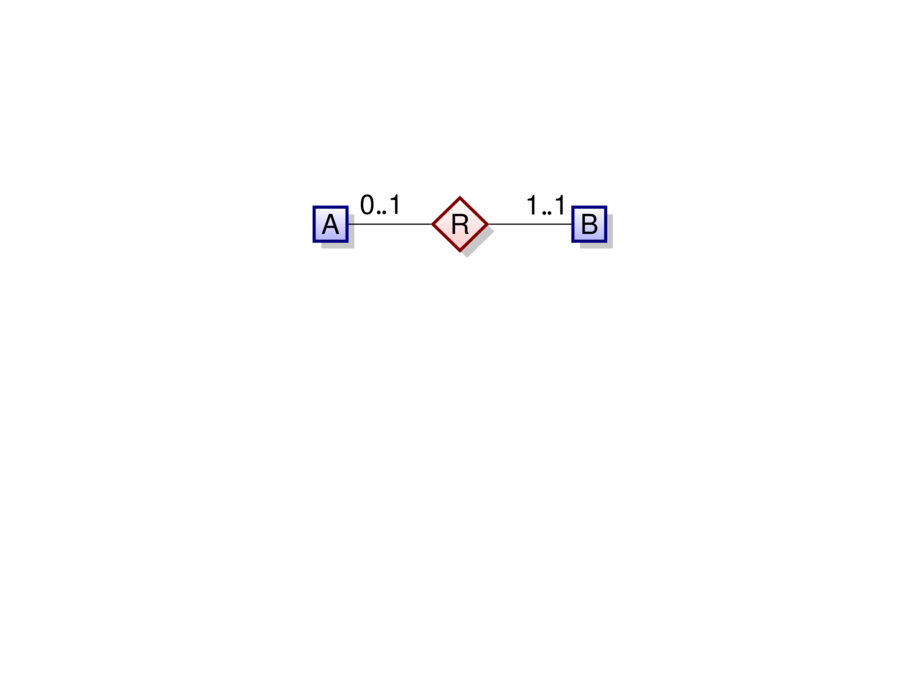
Every $a$ in $A$ is connected to one or more $b$ in $B$,\\
and every $b$ in $B$ is connected to at most one $a$ in $A$.
\end{quiz}
\pause
\begin{center}
\begin{tikzpicture}[every edge/.style={link},node distance=18mm,>=triangle 45]
\begin{scope}
\node[relationship] (R) {R};
\node (l) [left of=R,entity,minimum size=4mm] {A}; \draw (R) -- node[above,pos=.6] {$0\sldots 1$} (l);
\node (r) [right of=R,entity,minimum size=4mm] {B}; \draw (R) -- node[above,pos=.6] {$1\sldots *$} (r);
\end{scope}
\end{tikzpicture}
\end{center}
\pause
\begin{quiz}{\textwidth}{}
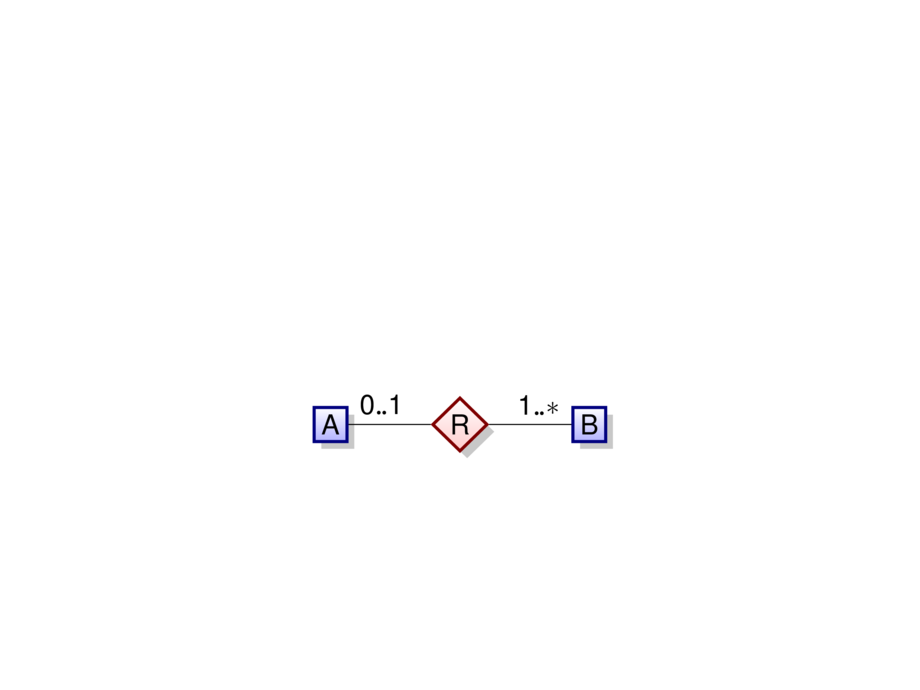
Every $a$ in $A$ is connected to one or more $b$ in $B$,\\
and every $b$ in $B$ is connected to precisely one $a$ in $A$.
\end{quiz}
\pause
\begin{center}
\begin{tikzpicture}[every edge/.style={link},node distance=18mm,>=triangle 45]
\begin{scope}
\node[relationship] (R) {R};
\node (l) [left of=R,entity,minimum size=4mm] {A}; \draw (R) -- node[above,pos=.7] {$1\sldots 1$} (l);
\node (r) [right of=R,entity,minimum size=4mm] {B}; \draw (R) -- node[above,pos=.6] {$1\sldots *$} (r);
\end{scope}
\end{tikzpicture}
\end{center}
\end{frame}

