\begin{frame}[t]
  \frametitle{Cardinality Limits: Many-to-Zero or One}
  
  \begin{center}\vspace{-1ex}
  \begin{tikzpicture}[every edge/.style={link},node distance=22mm,>=triangle 45]
    \begin{scope}
      \node[relationship] (R) {R};
      \node (l) [left of=R,entity,minimum size=4mm] {A}; \draw (R) -- node[above,pos=.6] {$0\sldots *$} (l); 
      \node (r) [right of=R,entity,minimum size=4mm] {B}; \draw (R) -- node[above,pos=.6] {$0\sldots 1$} (r);
      
      \begin{scope}[nodes={draw,rectangle,fill=green!20,minimum size=4mm,scale=.8}]
      \foreach \i in {1,2,3,4,5,6} {
        \node at (-12mm,-5mm*\i - 3mm) (a\i) {a\i};
        \node at (12mm,-5mm*\i - 3mm) (b\i) {b\i};
      }
      \end{scope}
      
      \begin{scope}[thick]
        \draw (a1) to[out=0,in=180] (b2);
        \draw (a4) to[out=0,in=180] (b3);
        \draw (a5) to[out=0,in=180] (b3);
        \draw (a6) to[out=0,in=180] (b3);
      \end{scope}
    \end{scope}
  \end{tikzpicture}\vspace{-.5ex}
  \end{center}
  \bigskip
  
  \begin{goal}{}
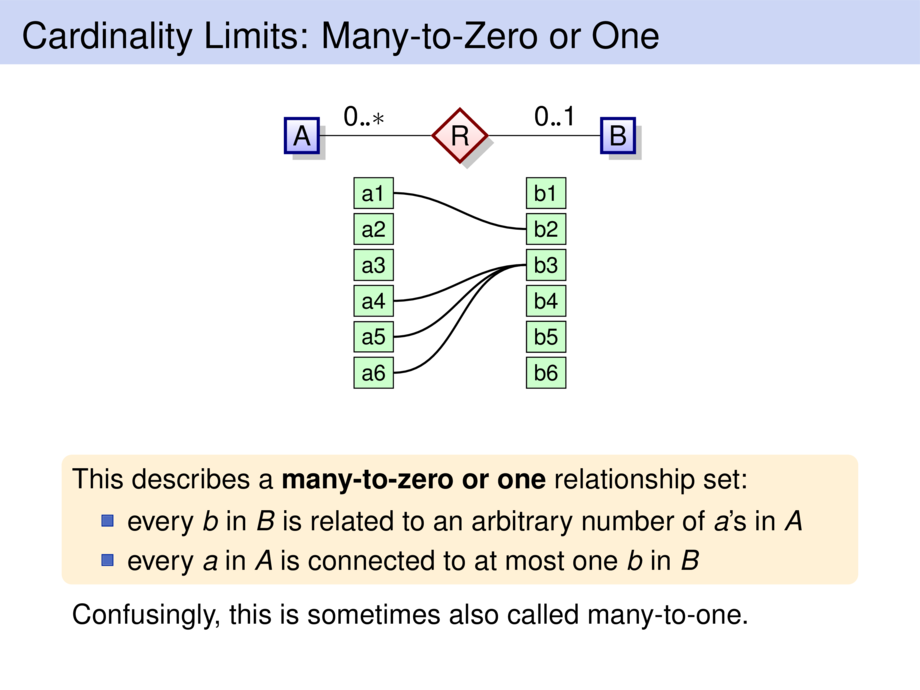
    This describes a \emph{many-to-zero or one} relationship set:
    \begin{itemize}
      \item every $b$ in $B$ is related to an arbitrary number of $a$'s in $A$
      \item every $a$ in $A$ is connected to at most one $b$ in $B$
    \end{itemize}
  \end{goal}
  Confusingly, this is sometimes also called many-to-one.
\end{frame}