


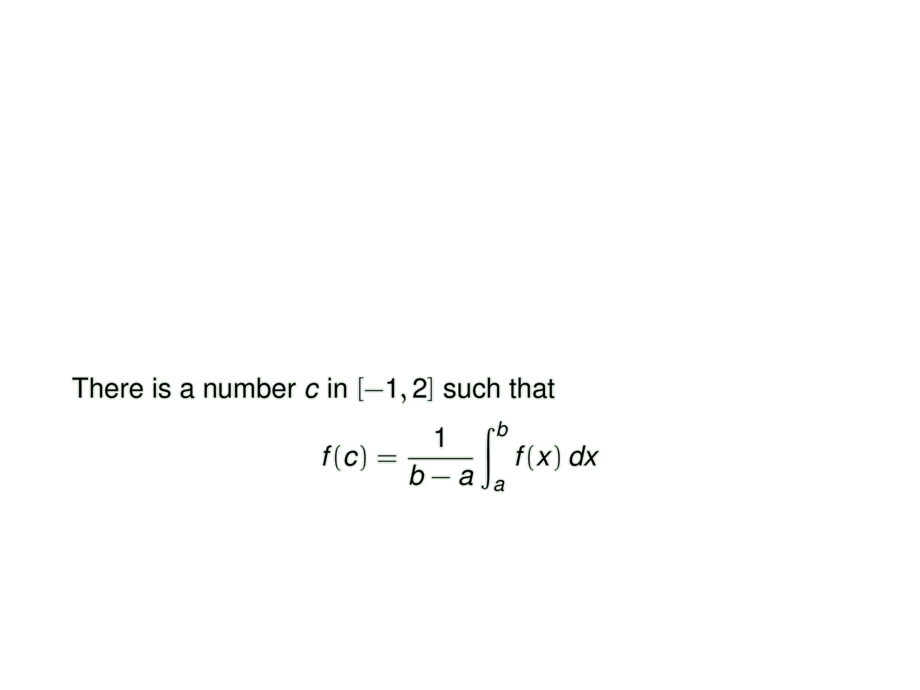
































































































44/50
\begin{frame}
\frametitle{Average Value of a Function}
\begin{block}{Mean Value Theorem \emph{for Integrals}}
If $f$ is continuous an $[a,b]$, then there is $c$ in $[a,b]$ such that:\vspace{-1ex}
\begin{talign}
f(c) \;=\; f_{\text{avg}} \;=\; \frac{1}{b-a} \int_a^b f(x) \, dx
\end{talign}
\end{block}
\pause\medskip
\begin{exampleblock}{}
Since $f(x) = 1+ x^2$ is continuous on $[-1,2]$,
the Mean Value Theorem for Integrals says\ldots
\pause
\medskip
There is a number $c$ in $[-1,2]$ such that
\begin{talign}
f(c) = \frac{1}{b-a} \int_a^b f(x) \, dx
\end{talign}
\pause
For this $f$, we can find $c$ explicitly. \pause Since $\frac{1}{b-a} \int_a^b f(x) \, dx = 2$
\pause
\begin{talign}
2 &= f(c) = 1+ c^2 \mpause[1]{\;\implies\; c^2 = 1} \mpause{\;\implies\; c = \pm 1}
\end{talign}
\pause\pause\pause
Thus there are two numbers $c = -1$ and $c= 1$ that work!
\end{exampleblock}
\vspace{10cm}
\end{frame}

