\begin{frame}
  \frametitle{Average Value of a Function}

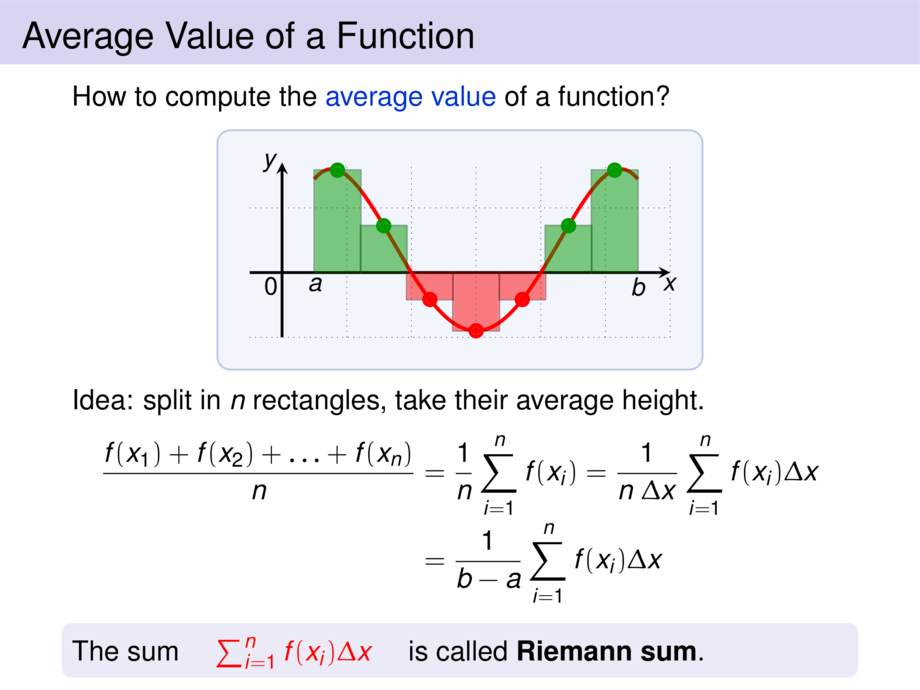
  How to compute the \textcolor{cblue}{average value} of a function?
  
  \begin{center}
  \scalebox{.9}{
  \begin{tikzpicture}[default]
    \def\mfun{(-.9 + (\x-3+\mfunshift)^2 - .1*(\x-3+\mfunshift)^4)}

    \diagram[1]{-.5}{6}{-1}{1.7}{1}
    \diagramannotatez
    \def\mfunshift{0}
    \begin{scope}[ultra thick]
      \draw[cred] plot[smooth,domain=.5:5.5,samples=100] (\x,{\mfun});
      \node[anchor=north] at (.5,0) {$a$};
      \node[anchor=north] at (5.5,0) {$b$};
      
      \only<1>{
      \draw[cblue] (.5,2.01042/5) -- (5.5,2.01042/5);
      }
      
      \only<2->{
      \def\mwidth{5}
      \foreach \nrsteps/\mcolor in {6/cred} {
        \def\mstep{\mwidth/(\nrsteps+1)}
        \def\mfunshift{.5*\mstep}
        \foreach \xx in {0,...,\nrsteps} {
          \def\x{.5+ \xx*\mstep}
          \pgfmathparse{{\mfun}}
          \ifthenelse{\lengthtest{\pgfmathresult cm > 0cm}}{
            \def\mcolor{cgreen}
          }{}
          \draw[thick,draw=\mcolor!60!black,fill=\mcolor,opacity=.5] ({\x},0) rectangle ({\x+\mstep},{\mfun}); 
          \node[include=\mcolor] at ({\x+\mfunshift},{\mfun}) {};
        }
      }
      }
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}\vspace{-.75ex}
  \pause
  Idea: split in $n$ rectangles, take their average height.
  \pause
  \begin{talign}
    \frac{f(x_1) + f(x_2) + \ldots + f(x_n)}{n} 
    \mpause[1]{ &= \frac{1}{n}\sum_{i = 1}^n f(x_i) }
    \mpause{= \frac{1}{n\;\Delta x}\sum_{i = 1}^n f(x_i)\Delta x} \\[-.5ex]
    \mpause{&= \frac{1}{b-a}\sum_{i = 1}^n f(x_i)\Delta x}
  \end{talign}\vspace{-1ex}
  \pause\pause\pause\pause
  
  \begin{block}{}
    The sum \quad \alert{$\sum_{i = 1}^n f(x_i) \Delta x$} \quad 
    is called \emph{Riemann sum}. 
  \end{block}
  \vspace{10cm}
\end{frame}