

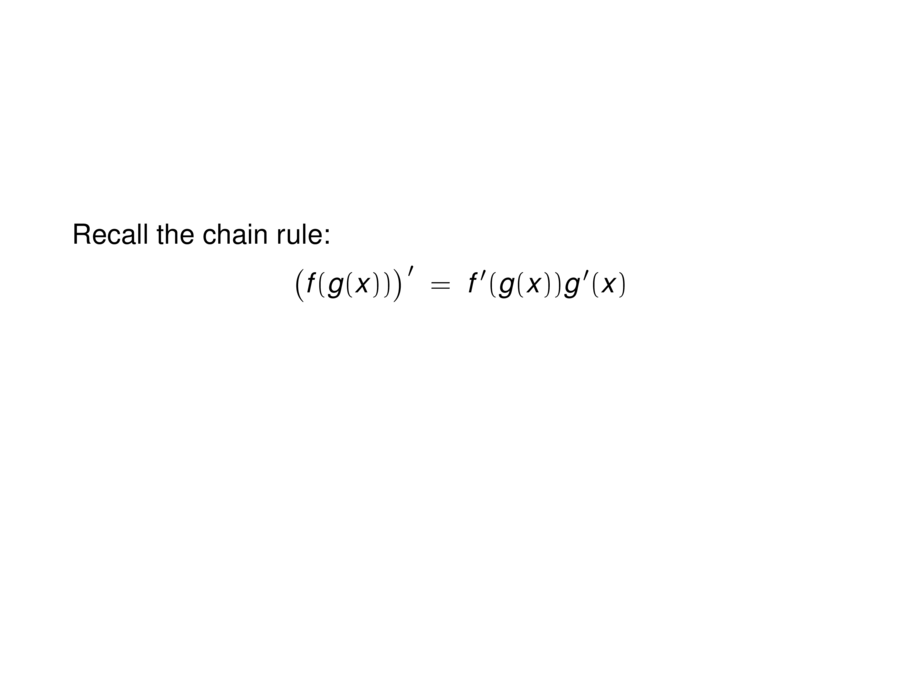

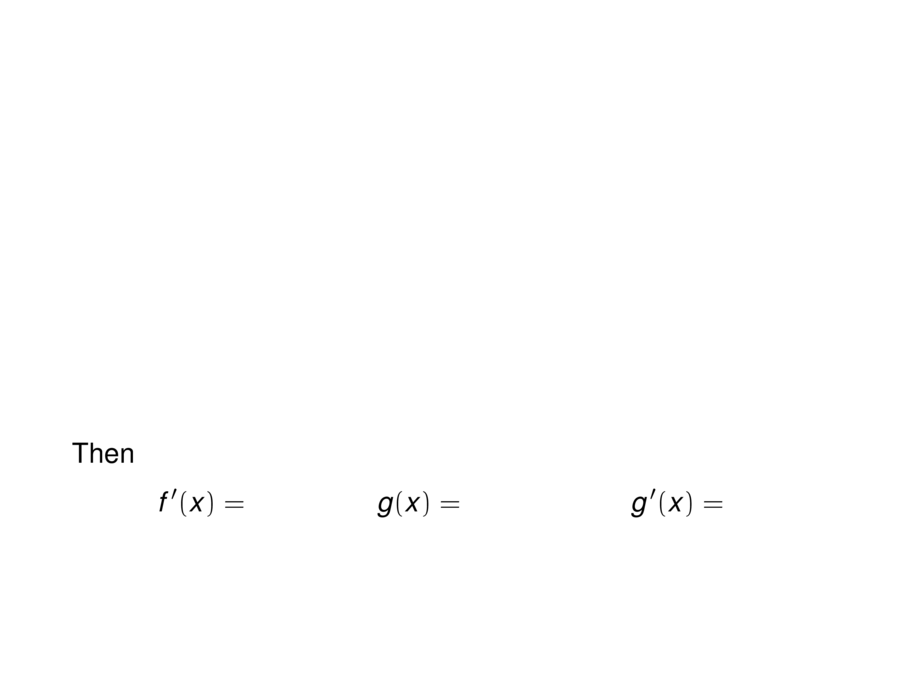































































































11/236
\begin{frame}
\frametitle{The Substitution Rule for Indefinite Integrals}
How to find antiderivatives of formulas like
\begin{talign}
\int 2x\sqrt{1 + x^2} dx \quad\text{?}
\end{talign}
\pause
Recall the chain rule:
\begin{talign}
\big( f(g(x)) \big)' \;=\; \alert<3->{f'(g(x)) g'(x)}
\end{talign}
\pause
Let us try to write the integral in the form:
\begin{talign}
\int f'(g(x)) g'(x) dx
\end{talign}
\pause
Then
\begin{talign}
f'(x) = \mpause[1]{\sqrt{x}}
&&
g(x) = \mpause{1 + x^2}
&&
g'(x) = \mpause{2x}
\end{talign}
\pause\pause\pause\pause
Moreover the antiderivative of $f'(x)$ is \quad $f(x) = \pause \frac{2}{3}x^{\frac{3}{2}}$
\pause. Thus
\begin{talign}
\int 2x\sqrt{1 + x^2} dx = \mpause[1]{ f(g(x)) + C } \mpause{= \frac{2}{3}(1+x^2)^{\frac{3}{2}} + C}
\end{talign}
\vspace{10cm}
\end{frame}

