\begin{frame}
  \frametitle{Review - Midterm Exam 3}

  \begin{exampleblock}{}
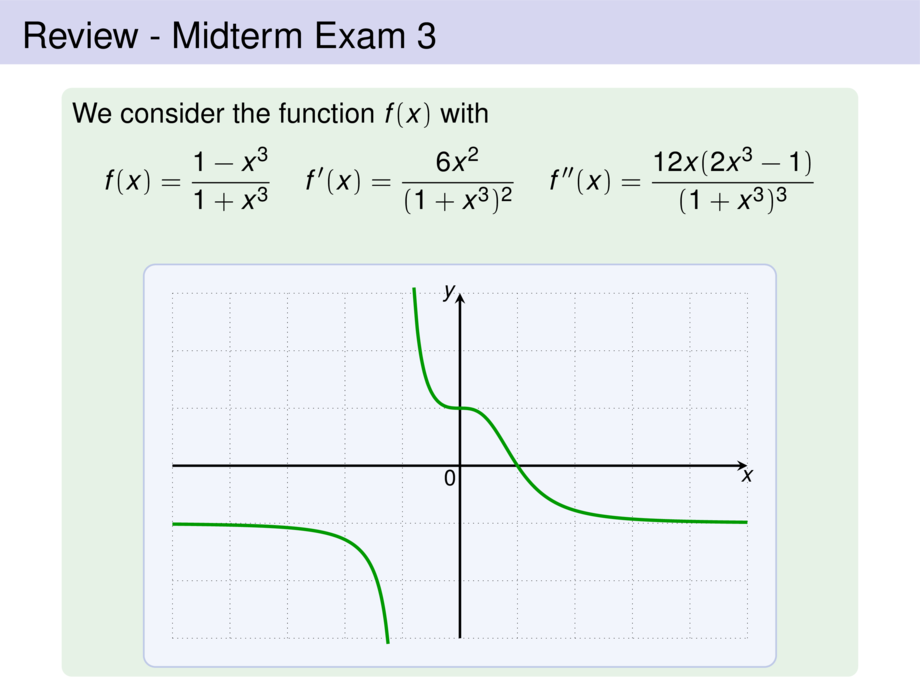
    We consider the function $f(x)$ with  
    \begin{talign}
      f(x) = \frac{1-x^3}{1+x^3}
      &&
      f'(x) = \frac{6x^2}{(1+x^3)^2}
      &&
      f''(x) = \frac{12x(2x^3-1)}{(1+x^3)^3}
    \end{talign}
    \only<-1>{
    Find all
    \begin{itemize}
      \item horizontal, vertical asymptotes,
      \item the left and right limits at vertical asymptotes,
      \item points with horizontal tangents and local extrema
      \item on which intervals is $f$ increasing/decreasing?
      \item on which intervals is $f$ concave up/down?
      \item inflection points
    \end{itemize}
    Then sketch the graph of $f(x)$.    
    }
    \only<2>{
      \begin{center}
      \scalebox{.8}{
      \begin{tikzpicture}[default]
        \diagram[1]{-5}{5}{-3}{3}{1}
        \diagramannotatez
        \def\mfunshift{0}
        \begin{scope}[ultra thick]
          \draw[cgreen] plot[smooth,domain=-5:-1.25,samples=100] function{(1-x**3)/(1+x**3)};
          \draw[cgreen] plot[smooth,domain=-.8:5,samples=100] function{(1-x**3)/(1+x**3)};
        \end{scope}
      \end{tikzpicture}
      }
      \end{center}
    }
  \end{exampleblock}
\end{frame}