



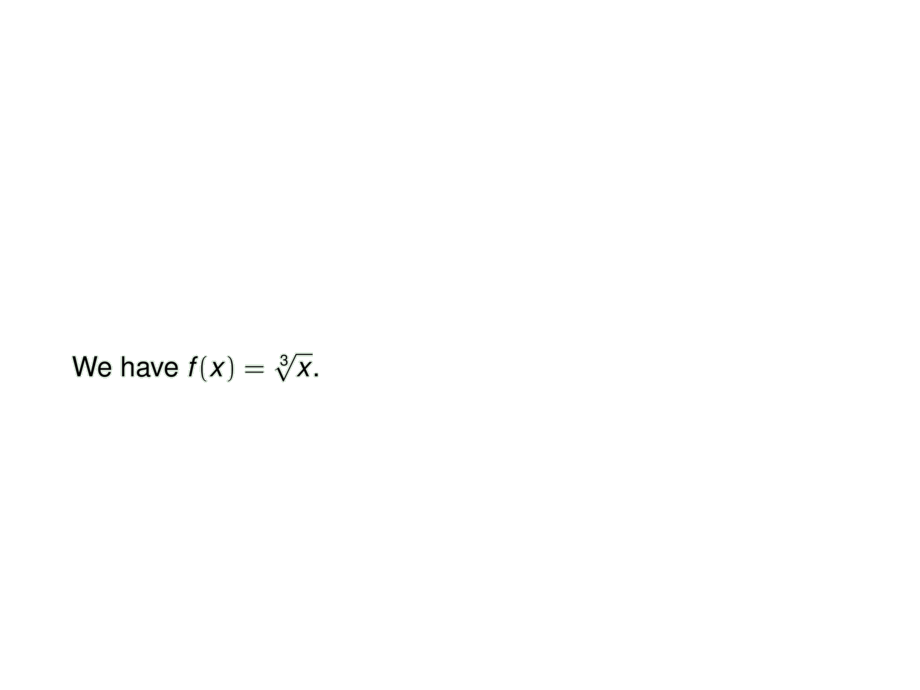






























































































160/176
\begin{frame}
\frametitle{Review - Midterm Exam 3}
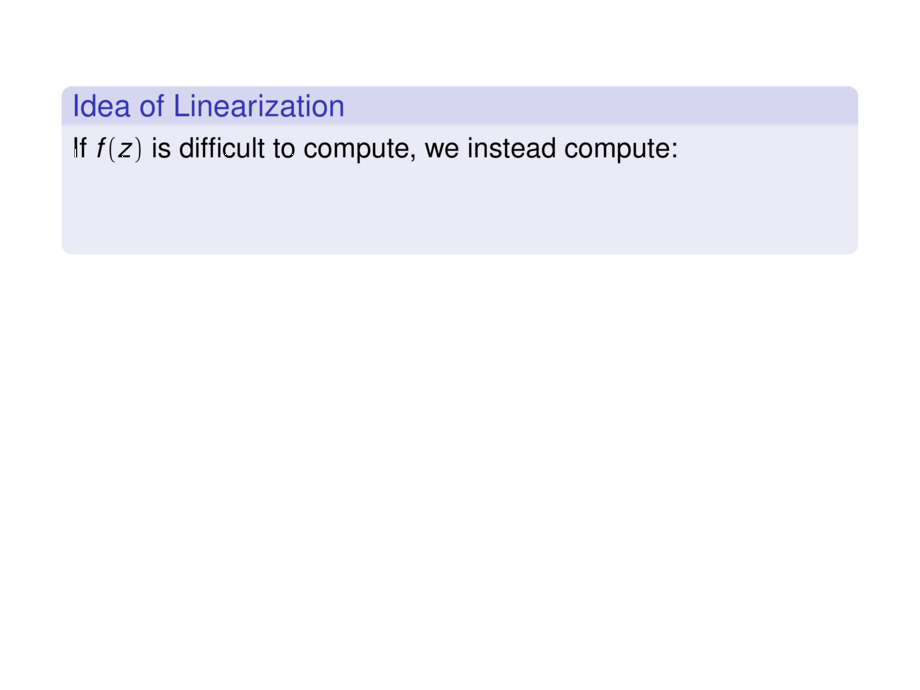
\begin{block}{Idea of Linearization}
If $f(z)$ is difficult to compute, we instead compute:
\begin{itemize}
\pause
\item tangent $L$ at a point $a$ near $z$ where $f(a)$ and $f'(a)$ are easy
\pause
\item then we approximate $f(z)$ by $L(z)$
\end{itemize}
\end{block}\pause
\begin{exampleblock}{}
Use differentials to approximate $\sqrt[3]{999}$.
\pause\bigskip
We have $f(x) = \sqrt[3]{x}$. \pause
%
We compute linearization at
$a = \pause 1000$.\pause
\begin{talign}
f(1000) &= \mpause[1]{10} \\
\mpause[2]{f'(x) }&\mpause[2]{= }\mpause[3]{\frac{1}{3}x^{-\frac{2}{3}} = \frac{1}{3(\sqrt[3]{x})^2}} &
\mpause[4]{f'(1000) = \frac{1}{3\cdot 10^2}}\mpause[5]{= \frac{1}{300}}
\end{talign}
\pause\pause\pause\pause\pause\pause
The linearization of $f$ at $1000$ is
$
L(x) = \pause 10 + \frac{1}{300}(x-1000)
$
\pause\medskip
Then the approximation of $\sqrt[3]{999}$ is:\vspace{-.7ex}
\begin{talign}
\sqrt[3]{999} \approx
\mpause[1]{L(999)}
&\mpause[2]{= 10 + \frac{1}{300}(999-1000)}
\mpause[3]{= 10 - \frac{1}{300}}
\end{talign}
\end{exampleblock}
\end{frame}

