


































































































24/81
\begin{frame}
\frametitle{Fundamental Theorem of Calculus}
\fundamental
\pause\medskip
\begin{exampleblock}{}
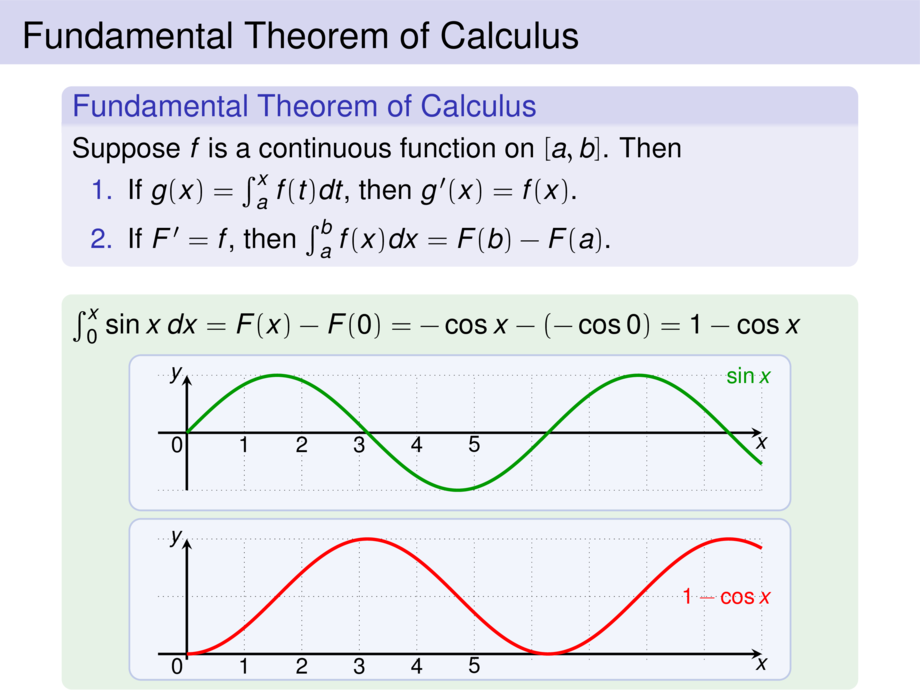
$\int_0^x \sin x\, dx = \mpause[1]{F(x) - F(0)} \mpause{= -\cos x - (-\cos 0)} \mpause{= 1-\cos x}$ \vspace{-1ex}
%\mpause[2]{here $F(x) = -\cos x$}?\vspace{-1ex}
\begin{center}
\scalebox{.8}{
\begin{tikzpicture}[default]
\def\diabordery{.35cm}
\diagram[1]{-.5}{10}{-1}{1}{1}
\diagramannotatez
\diagramannotatex{1,2,3,4,5}
\begin{scope}[ultra thick,cgreen]
\draw plot[smooth,domain=0:10,samples=100] function{sin(x)};
\node[anchor=east] at (10.25,1) {$\sin x$};
\end{scope}
\end{tikzpicture}
}\\[.3ex]\pause\pause\pause\pause
\scalebox{.8}{
\begin{tikzpicture}[default]
\def\diabordery{.35cm}
\diagram[1]{-.5}{10}{-.1}{2}{1}
\diagramannotatez
\diagramannotatex{1,2,3,4,5}
\begin{scope}[ultra thick,cred]
\draw plot[smooth,domain=0:10,samples=100] function{-cos(x)+1};
\node[anchor=east] at (10.25,1) {$1-\cos x$};
\end{scope}
\end{tikzpicture}
}
\end{center}
\end{exampleblock}
\end{frame}

