
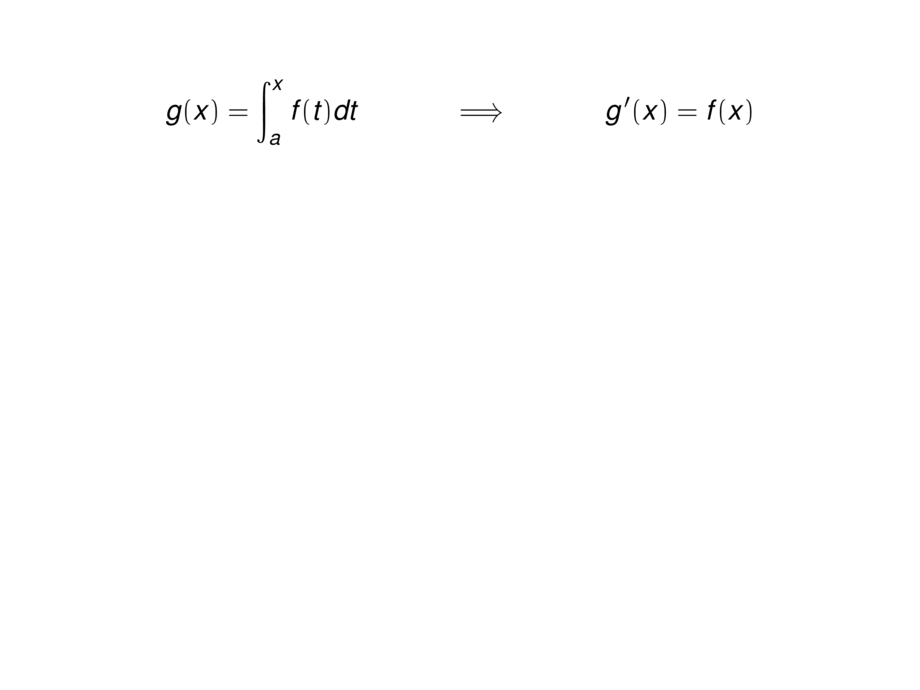

































































































11/81
\begin{frame}
\frametitle{Fundamental Theorem of Calculus}
\vspace{-3ex}
\begin{talign}
g(x) = \int_a^x f(t)dt &&\implies&& g'(x) = f(x)
\end{talign} \vspace{-1ex}
\pause
\scalebox{.8}{
\begin{tikzpicture}[default]
\diagram[1]{-1}{4}{-0}{6.5}{1}
\diagramannotatez
\diagramannotatex{1,2,3}
\diagramannotatey{1,2,3,3}
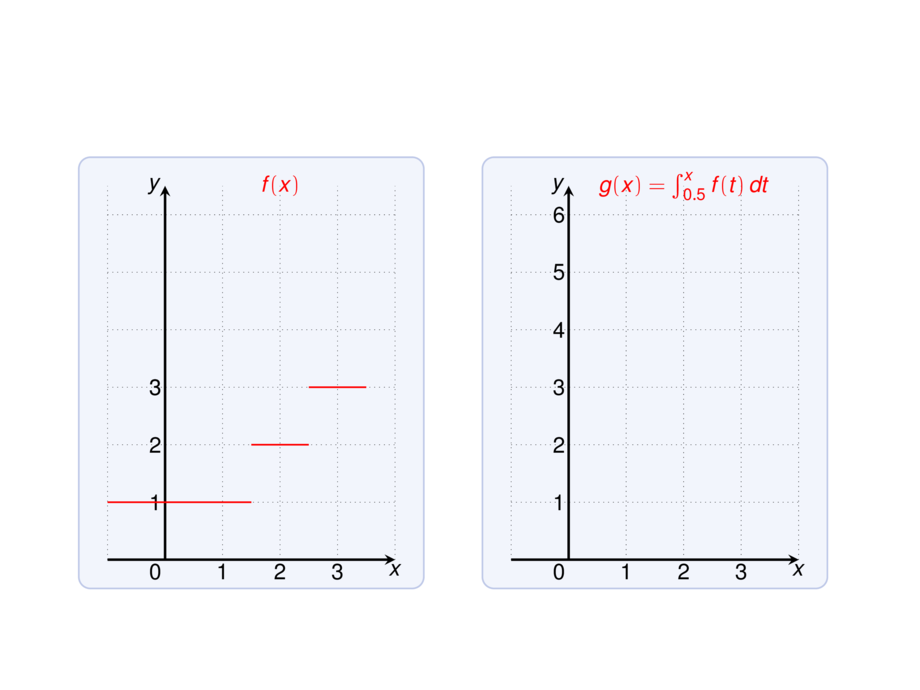
\node[cred] at (2,6.5) {$f(x)$};
\draw[cred] plot[smooth,domain=-1:1.5,samples=20] (\x,{1});
\draw[cred] plot[smooth,domain=1.5:2.5,samples=20] (\x,{2});
\draw[cred] plot[smooth,domain=2.5:3.5,samples=20] (\x,{3});
\onslide<3->{ \draw[draw=none,fill=cred,opacity=.5] plot[ybar interval,domain=0.5:1.5,samples=2] (\x,{1}); }
\onslide<4->{ \draw[draw=none,fill=cred,opacity=.5] plot[ybar interval,domain=1.5:2.5,samples=2] (\x,{2}); }
\onslide<5>{ \draw[draw=none,fill=cred,opacity=.5] plot[ybar interval,domain=2.5:3.5,samples=2] (\x,{3}); }
\onslide<6->{
\draw[draw=none,fill=cred,opacity=.5] plot[ybar interval,domain=2.5:3,samples=2] (\x,{3});
\draw[dashed,cblue] (3,-.5) -- node [at end,above] {$x = 3$} (3,6.5);
\node at (1.75,.5) {area = $4.5$};
}
\begin{scope}[xshift=.65\textwidth]
\diagram[1]{-1}{4}{-0}{6.5}{1}
\diagramannotatez
\diagramannotatex{1,2,3}
\diagramannotatey{1,2,3,4,5,6}
\node[cred] at (2,6.5) {$g(x) = \int_{0.5}^x f(t)\,dt$};
\pause
\node[cred,include] at (1.5,1) {};
\draw[cred] plot[smooth,domain=0.5:1.5,samples=20] (\x,{\x-.5});
\pause
\node[cred,include] at (2.5,3) {};
\draw[cred] plot[smooth,domain=1.5:2.5,samples=20] (\x,{2*\x-2});
\pause
\node[cred,include] at (3.5,6) {};
\draw[cred] plot[smooth,domain=2.5:3.5,samples=20] (\x,{3*\x-4.5});
\pause
\node[include,cblue] at (3,4.5) {};
\draw[dashed,cblue] (3,-.5) -- (3,6.5); % node [at end,above] {$x = 3$}
\end{scope}
\begin{scope}[line width=2mm,cgreen,->,xshift=.5cm]
\onslide<7->{
\draw[opacity=.7] (1.5,1) to[bend left=23] (9,4.3);
\path[decoration={text along path,raise=2mm,text={area = integral\ \ \ \ \ \ },text align={center}},decorate] (1.5,1) to[bend left=23] (9,4.3);
}
\onslide<8->{
\draw[opacity=.7] (9,4.9) to[bend left=-25] (2.9,3.4);
\path[decoration={text along path,raise=2mm,text={slope = derivative\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ },text align={center}},decorate] (2.9,3.4) to[bend left=25] (9,4.9);
}
\end{scope}
\pause
\pause
\pause
\end{tikzpicture}
}\smallskip
\mpause[0]{
Observe: $g'(x) = f(x)$ except where $f$ is not continuous.\vspace{-.75ex}
}
\mpause[1]{
\begin{alertblock}{}
The slope (derivative) is the inverse of taking the area (integral).
\end{alertblock}
}
\vspace{10cm}
\end{frame}

