
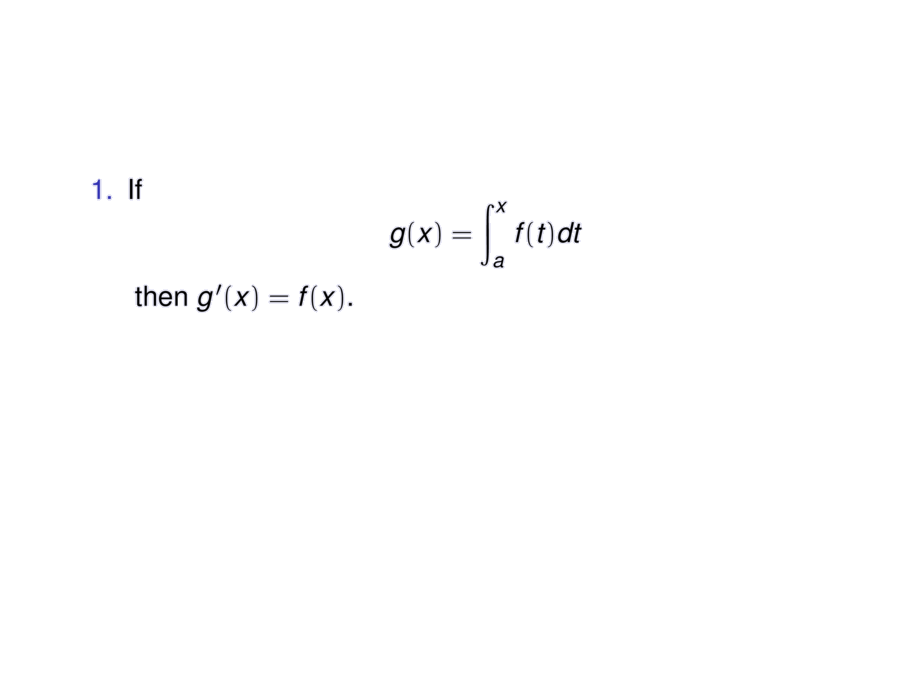
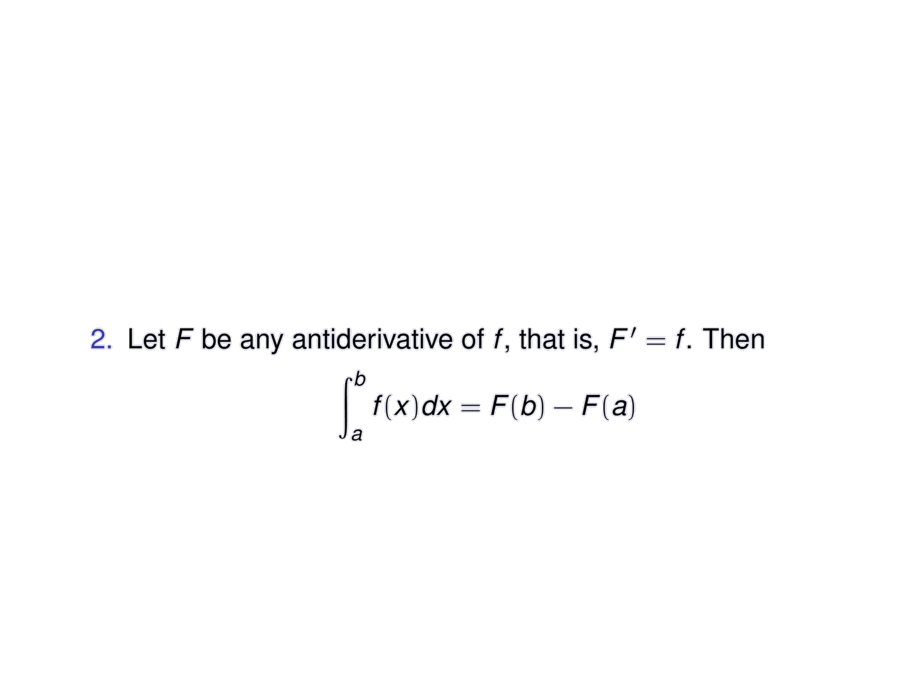
































































































7/81
\begin{frame}
\frametitle{Fundamental Theorem of Calculus}
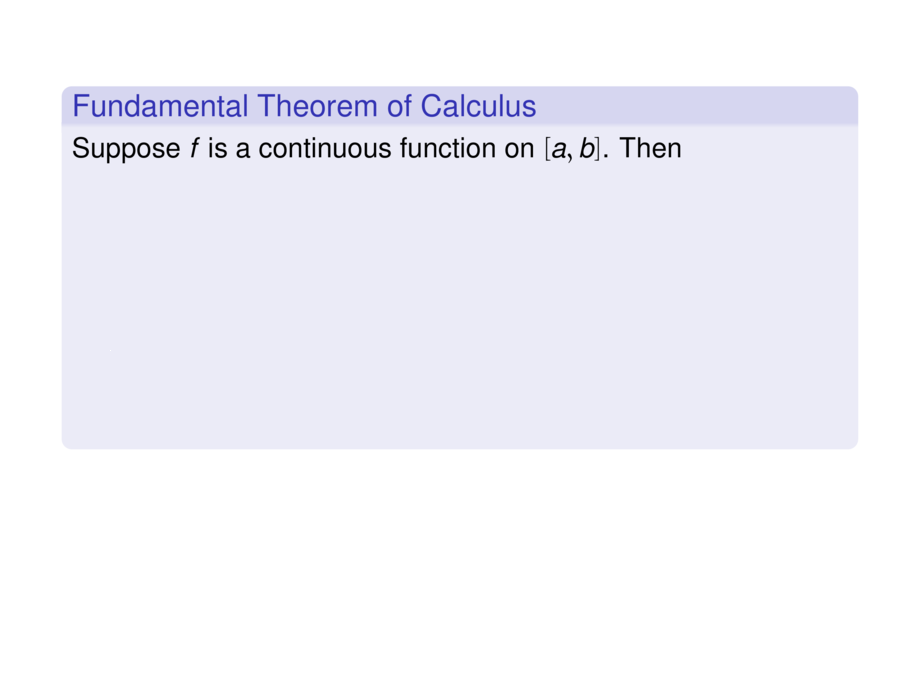
\begin{block}{Fundamental Theorem of Calculus}
Suppose $f$ is a continuous function on $[a,b]$. Then
\begin{enumerate}
\pause
\item If \vspace{-1ex}
\begin{talign}
g(x) = \int_a^x f(t)dt\,
\end{talign} \vspace{-1ex}
then $g'(x) = f(x)$.
\medskip\pause
\item Let $F$ be any antiderivative of $f$, that is, $F' = f$. Then
\begin{talign}
\int_a^b f(x)dx = F(b) - F(a)
\end{talign}
\end{enumerate}
\end{block}
\pause\medskip
The first part of the theorem can be written as:\vspace{-1ex}
\begin{talign}
\frac{d}{dx} \int_a^x f(t)dt = f(x)
\end{talign}
\pause
The second part can be written as:\vspace{-1ex}
\begin{talign}
\int_a^b F'(x)dx = F(b) - F(a)
\end{talign}
\end{frame}

