\begin{frame}
  \frametitle{The Area below a Curve}

  \begin{exampleblock}{}
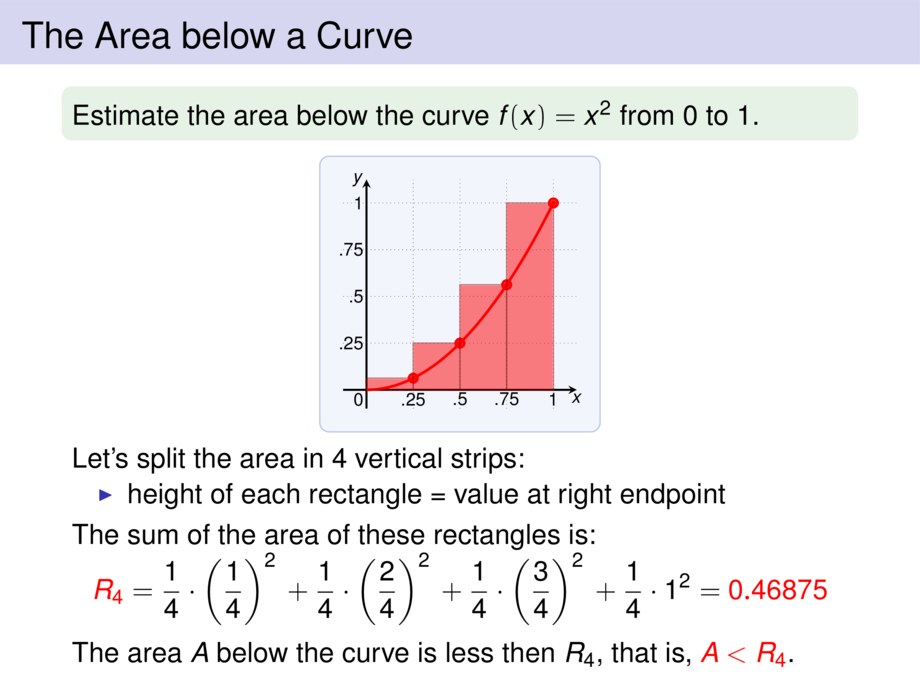
    Estimate the area below the curve $f(x) = x^2$ from $0$ to $1$.
  \end{exampleblock}
  
  \begin{center}
  \scalebox{.65}{
  \begin{tikzpicture}[default]
    \def\mfun{(4*((\x+\mfunshift)/4)^2)}

    \diagram[1]{-.5}{4.5}{-.4}{4.5}{1}
    \diagramannotatez
    \diagramannotatexx{1/.25,2/.5,3/.75,4/1}
    \diagramannotateyy{1/.25,2/.5,3/.75,4/1}
    \def\mfunshift{0}
    \begin{scope}[ultra thick]
      \draw[cred] plot[smooth,domain=0:4,samples=20] (\x,{\mfun});

      \def\mwidth{4}
      \setcounter{slide}{2}
      \foreach \nrsteps/\mcolor in {3/cred} {
        \setcounter{roundcounter}{\arabic{slide}}
        \def\mstep{\mwidth/(\nrsteps+1)}
        \def\mfunshift{0}
        \foreach \xx in {0,...,\nrsteps} {
          \def\x{\xx*\mstep}
          \setcounter{tmpcount}{\arabic{roundcounter}}
          \addtocounter{tmpcount}{\nrsteps}
          \onslide<\arabic{slide}->{ 
            \draw[thick,draw=\mcolor!60!black,fill=\mcolor,opacity=.5] ({\x},0) rectangle ({\x+\mstep},{\mfun}); 
            \node[include=\mcolor] at ({\x+\mfunshift},{\mfun}) {};
          }
          \addtocounter{slide}{1}
        }
      }
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
  \vspace{-1ex}
  
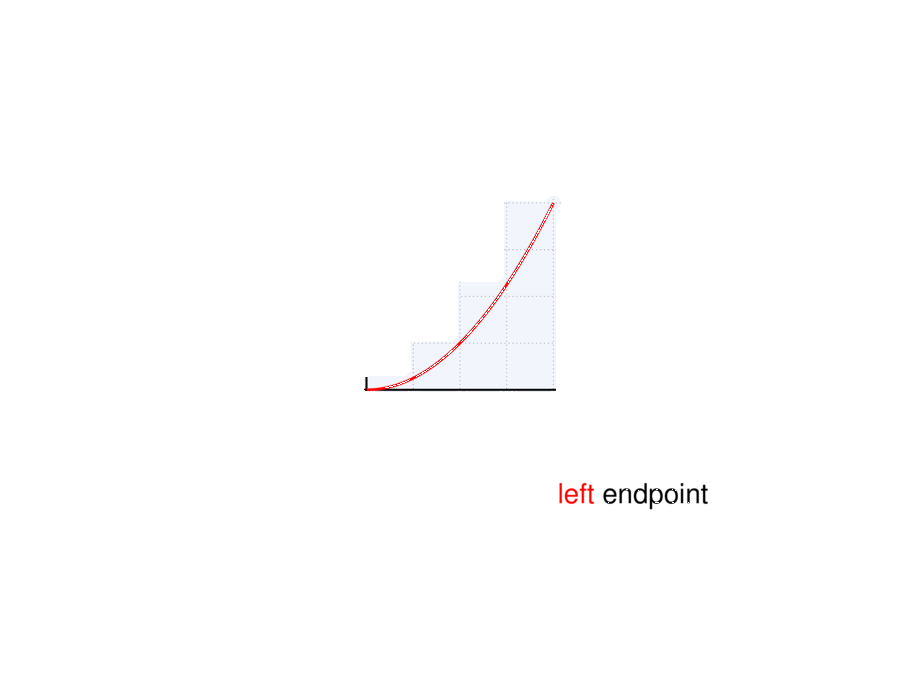
  Let's split the area in $4$ vertical strips:
  \begin{itemize}
    \item height of each rectangle = value at \alert{left} endpoint
  \end{itemize}
  \pause\pause\pause\pause\pause\smallskip
  
  The sum of the area of these rectangles is:\vspace{-1ex}
  \begin{talign}
    &\alert{L_4} = \mpause[1]{ \frac{1}{4} \cdot 0^2 }
    \mpause{ + \frac{1}{4} \cdot \left(\frac{1}{4}\right)^2 }
    \mpause{ + \frac{1}{4} \cdot \left(\frac{2}{4}\right)^2 }
    \mpause{ + \frac{1}{4} \cdot \left(\frac{3}{4}\right)^2 } 
    \mpause{ = \alert{0.21875}}
  \end{talign}
  \pause\pause\pause\pause\pause\pause
  The area $A$ below the curve is \pause larger then $L_4$, that is, \alert{$L_4 < A$}.

  \vspace{10cm}
\end{frame}