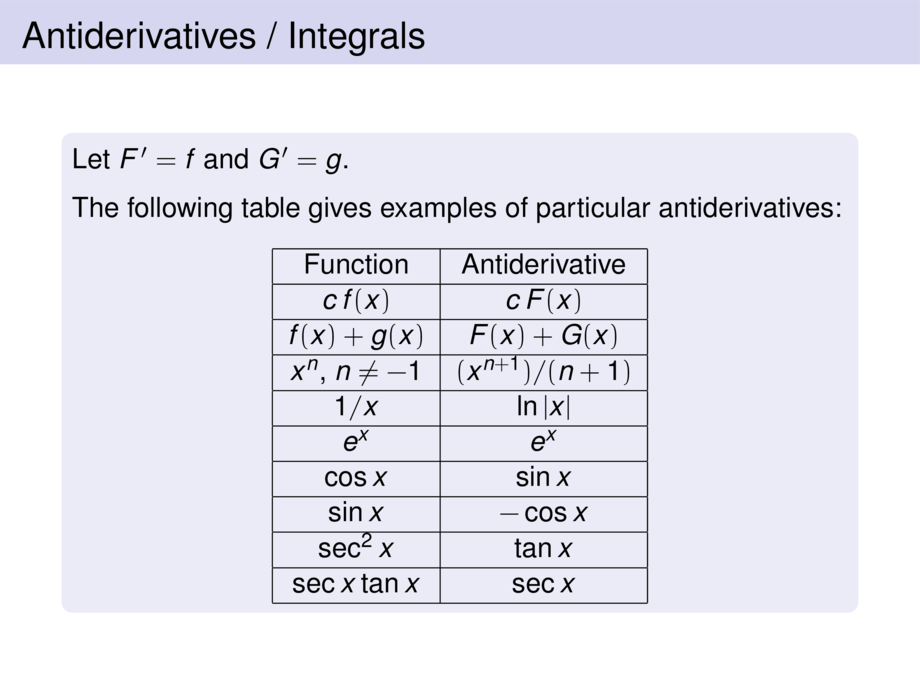

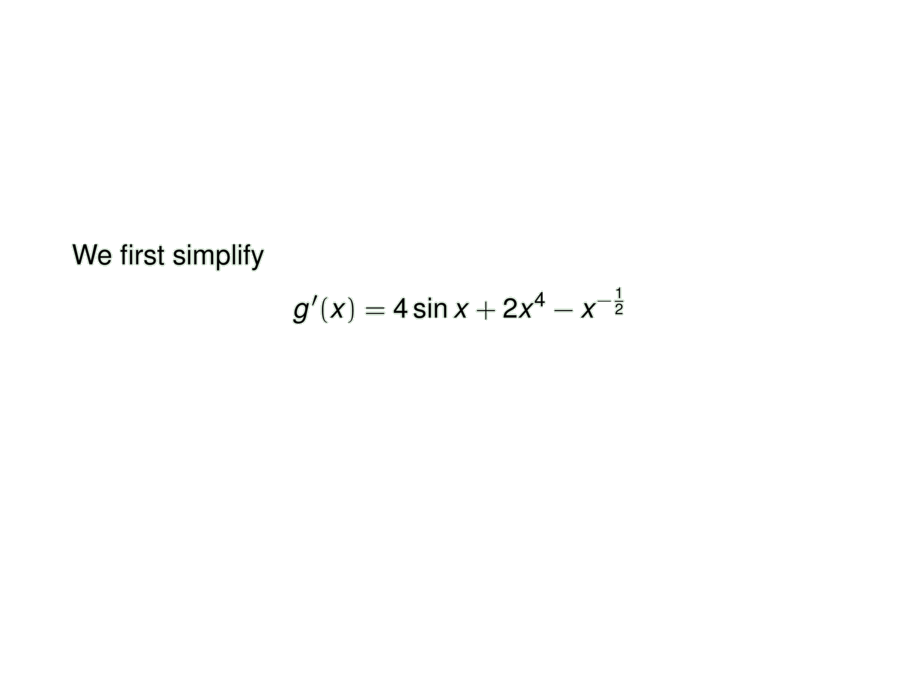

































































































48/116
\begin{frame}
\frametitle{Antiderivatives / Integrals}
\begin{exampleblock}{}
Find all functions $g$ such that
\begin{talign}
g'(x) = 4\sin x + \frac{2x^5 - \sqrt{x}}{x}
\end{talign}
\pause
We first simplify
\begin{talign}
g'(x) = 4\sin x + 2x^4 - x^{-\frac{1}{2}}
\end{talign}
\pause
Then the general antiderivative of $g'$ is:
\begin{talign}
g(x) = \mpause[1]{4(-\cos x)}\mpause{+ \frac{2}{5}x^5} \mpause{ - 2\sqrt{x}} \mpause{+ C}
\end{talign}
\end{exampleblock}
\pause\pause\pause\pause\pause\bigskip
In applications of calculus, finding antiderivatives is common:
\begin{itemize}
\pause
\item we measure the speed, and want the distance traveled
\pause
\item we measure the acceleration, and wand to know the speed
\pause
\item \ldots
\end{itemize}
\end{frame}

