



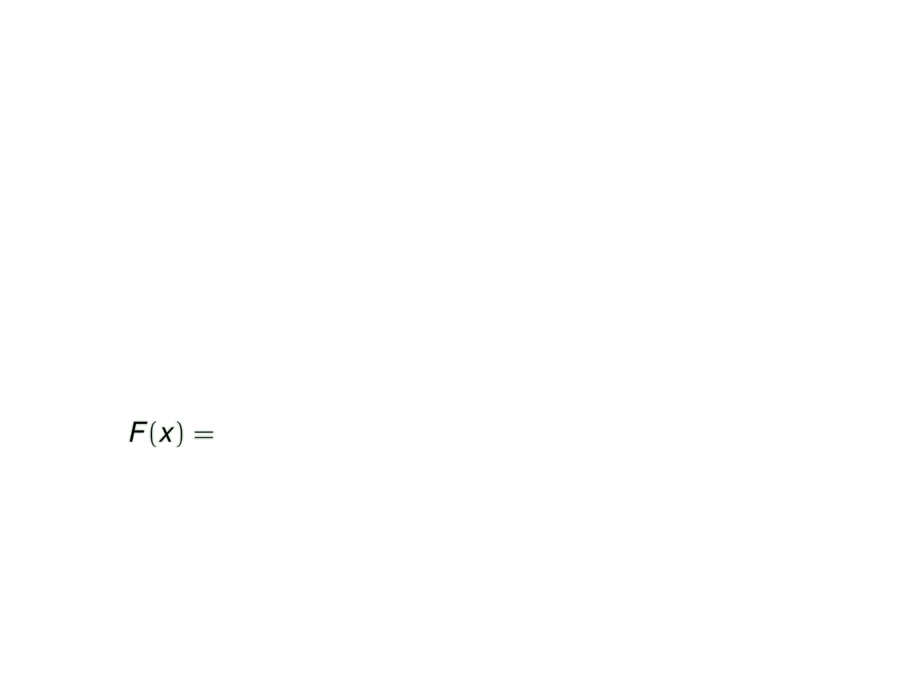

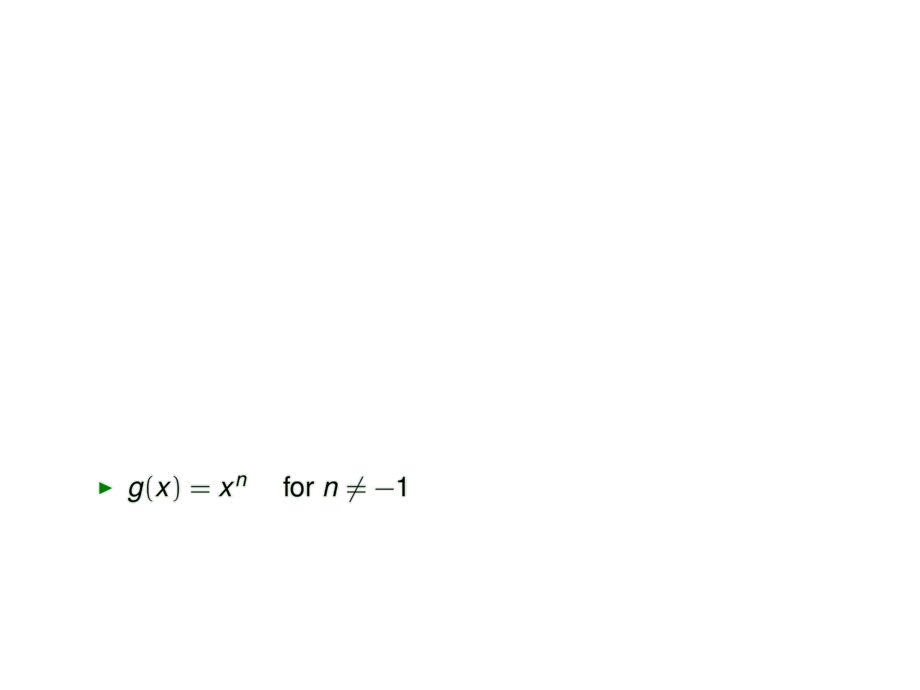





























































































16/116
\begin{frame}
\frametitle{Antiderivatives / Integrals}
\begin{block}{}
If $F$ is an antiderivative of $f$ on an interval $I$, \\
then the \emph{most general antiderivative} of $f$ on $I$ is
\begin{talign}
F(x) + C
\end{talign}
where $C$ is an arbitrary constant.
\end{block}
\pause
\begin{exampleblock}{}
Find the general antiderivatives of the following functions:
\begin{itemize}
\pause
\item $f(x) = \sin x$\\
\pause\medskip
$F(x) = \pause -\cos x + C$
\pause\medskip
\item $g(x) = x^n$ \quad for $n \ne -1$\\
\pause\medskip
$G(x) = \pause \frac{1}{n+1}x^{n+1} + C$
\pause\medskip
If $n \ge 0$, then this is valid for any interval.
\\\pause
If $n < 0$ \& $n \ne -1$, then valid for intervals not containing $0$.
\end{itemize}
\end{exampleblock}
\end{frame}

