\begin{frame}
  \frametitle{Newton's Method}


  \begin{block}{Newton's Method}
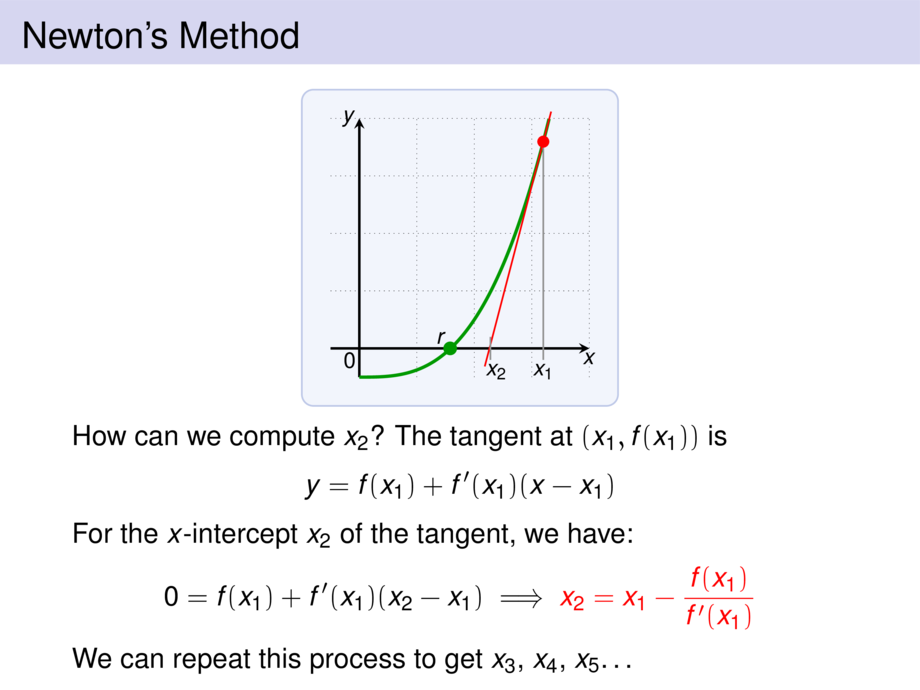
    Let $f(x)$ be a function, and $x_1$ and approximation of a root $r$.
    \pause\medskip
    
    We compute a sequence $x_2,x_3,x_4,\ldots$ of approximations by
    \begin{talign}
      x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
    \end{talign}
    \pause
    The hope is that $x_2,x_3,\ldots$ get closer and closer to the root $r$.
    \\\pause
    \onslide<18->{\alert{However, this does not always work.}}
  \end{block}
  \pause
  
  \only<-17>{
  \begin{exampleblock}{}
    Let $x_1 = 2$. Find the 3rd approximation to the root of $x^2-1$.
    \pause
    \begin{talign}
      f'(x) &= 2x\\[-.75ex]
      \mpause[1]{x_2 &=} 
        \mpause{ x_1 - \frac{f(x_1)}{f'(x_1)} }
        \mpause{= 2 - \frac{f(2)}{f'(2)} }
        \mpause{= 2 - \frac{3}{4} }
        \mpause{= \frac{5}{4} = 1.25 } \\[-.5ex]
      \mpause{x_3 &=} 
        \mpause{ x_2 - \frac{f(x_2)}{f'(x_2)} }
        \mpause{= \frac{5}{4} - \frac{f(\frac{5}{4})}{f'(\frac{5}{4})} }
        \mpause{= \frac{5}{4} - \frac{\left(\frac{5}{4}\right)^2-1}{\frac{10}{4}} }
        \mpause{= \frac{41}{40} = 1.025 }\\[-3.75ex]
    \end{talign}
    \pause\pause\pause\pause\pause\pause\pause\pause\pause\pause\pause
    The sequence $x_1,x_2,x_3,\ldots$ gets closer and closer to the root $1$.
  \end{exampleblock}
  }
  \only<18-25>{
    \pause[18]
    \begin{exampleblock}{}
    Let $x_1 = 1$. Find the 2nd approximation to the root of $\sqrt[3]{x}$.
    \pause
    \begin{minipage}{.49\textwidth}
    \begin{talign}
      f'(x) &= \frac{1}{3\sqrt[3]{x^2}} \\
      \mpause[1]{x_2 &=} 
        \mpause{1 - \frac{f(1)}{f'(1)} }
        \mpause{= 1 - \frac{1}{\left(\frac{1}{3}\right)} }
        \mpause{= -2 }
    \end{talign}
    \pause\pause\pause\pause\pause
    \end{minipage}~%
    \begin{minipage}{.49\textwidth}
      \smallskip
      \begin{center}
      \scalebox{.8}{
      \begin{tikzpicture}[default,baseline=1cm]
        \def\diabordery{.25cm}
        \def\diaborderx{.25cm}
        \diagram{-3}{2}{-1.4}{1.3}{1}
        \diagramannotatez
        \begin{scope}[ultra thick]
          \draw[cgreen,ultra thick] plot[smooth,domain=0:2,samples=200] function{x**(1/3.)};
          \draw[cgreen,ultra thick] plot[smooth,domain=-3:0,samples=200] function{-(-x)**(1/3.)};
          \node[include=cgreen] (r) at (0,0) {};
          \node[anchor=south east] at (r) {$r$};
        \end{scope}
        \draw[gray] (1,-.2) -- node[at start,below,black] {$x_1$} node[include=cred,at end] {} (1,1);
        \tangent{4.2cm}{1cm}{pow(\x,1/3)}{1}
        \draw[gray] (-2,-.2) -- node[at end,above,black] {$x_2$} (-2,.2);
      \end{tikzpicture}
      }
      \end{center}
    \end{minipage}
    \pause\vspace{.2ex}
    
    Note that $x_2 = -2$ is further away from the root $0$ than $x_1 = 1$.
    \end{exampleblock}
  }
  \only<26>{
    \vspace{1.2cm}
    \begin{exampleblock}{}
      For more complicated examples see 
      \begin{itemize}
        \item Chapter 4.8, Examples 1,2 and 3
      \end{itemize}
    \end{exampleblock}
  }
  \vspace{10cm}
\end{frame}