\begin{frame}
  \frametitle{Newton's Method}
  
  \begin{center}
  \scalebox{.8}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{4}{-.5}{4}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cgreen,ultra thick] plot[smooth,domain=-0:3.3,samples=200] function{-.5 + (.5*x)**3};
      \node[include=cgreen] (r) at (1.58,0) {};
      \node[anchor=south east] at (r) {$r$};
    \end{scope}
    \mpause[1]{
      \draw[gray] (3.2,-.2) -- node[at start,below,black] {$x_1$} node[include=cred,at end] {} (3.2,{-.5 + (.5*3.2)^3});
    }
    \mpause{
      \tangent{4cm}{.5cm}{-.5 + (.5*\x)^3}{3.2}
    }
    \mpause{
      \draw[gray] (2.28,-.2) -- node[at start,below,xshift=1mm,black] {$x_2$} (2.28,.2);
    }
  \end{tikzpicture}
  }
  \end{center}

  \begin{exampleblock}{Idea of Newton's Method}
    \begin{itemize}
    \pause
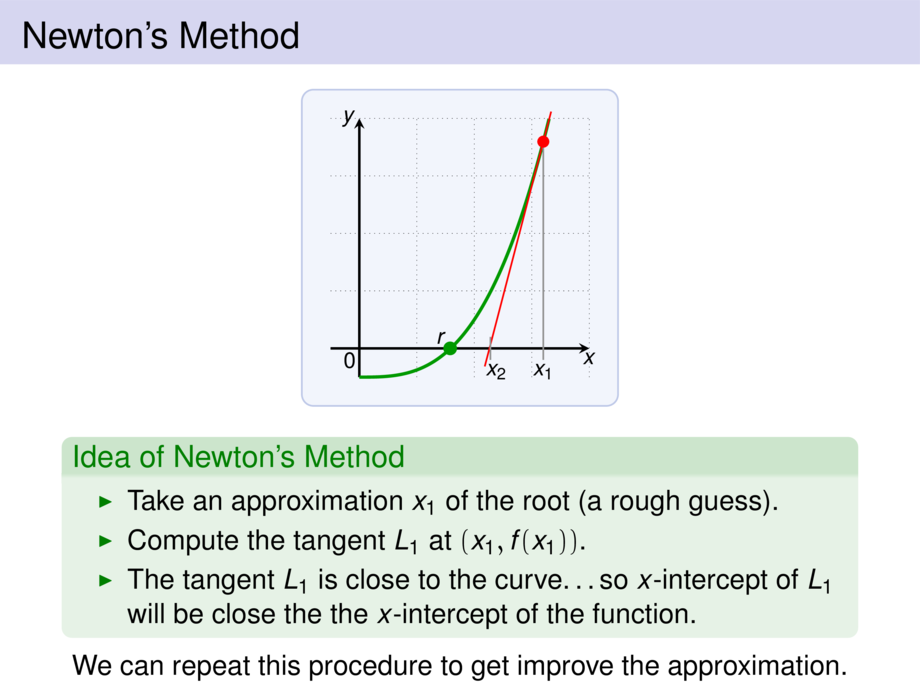
      \item Take an approximation $x_1$ of the root (a rough guess).
    \pause
      \item Compute the tangent $L_1$ at $(x_1,f(x_1))$.
    \pause
      \item The tangent $L_1$ is close to the curve\ldots
        so $x$-intercept of $L_1$ will be close the the $x$-intercept of the function.
    \end{itemize}
  \end{exampleblock}
  \pause
  We can repeat this procedure to get improve the approximation.
  \vspace{10cm}
\end{frame}