\begin{frame}
  \frametitle{Optimization}

  \vspace{-1ex}
  \begin{exampleblock}{}
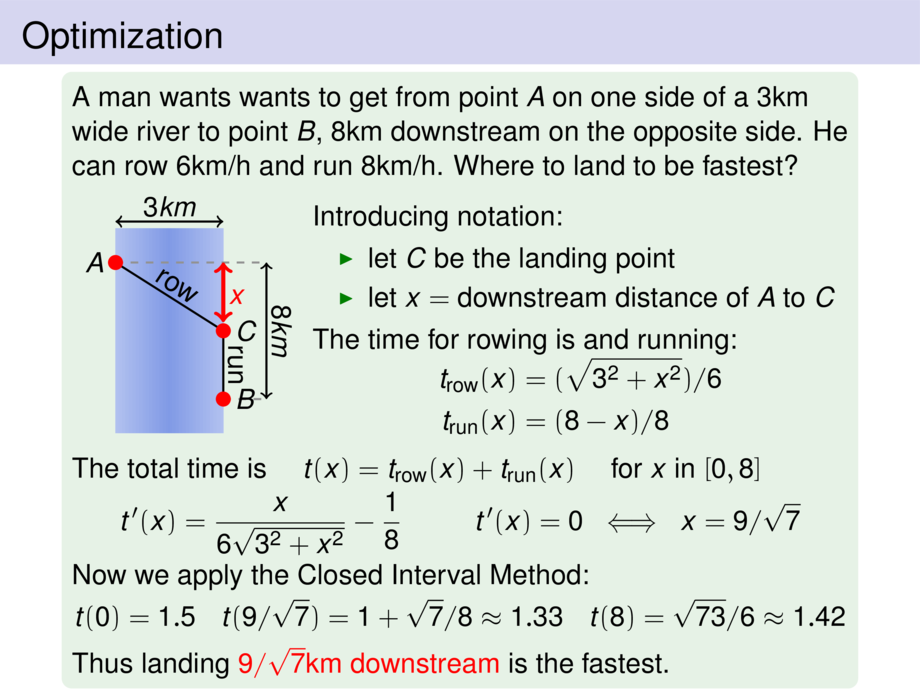
    A man wants wants to get from point $A$ on one side of a $3$km wide river
    to point $B$, $8$km downstream on the opposite side.
    He can row $6$km/h and run $8$km/h. Where to land to be fastest?
    \pause\medskip
    
    \begin{minipage}{.3\textwidth}
    \begin{center}
      \begin{tikzpicture}[default,yscale=.95]
        \draw[draw=none,shade,left color=cblue!30,right color=cblue!50] (0,0) rectangle (.75,3);
        \draw[draw=none,shade,right color=cblue!30,left color=cblue!50] (.74,0) rectangle (1.5,3);
        \mpause[1]{
          \draw (0,2.5) -- node[above,sloped] {row} (1.5,1.5) -- node[above,sloped] {run} (1.5,.5);
        }
        \mpause{
          \draw[<->] (0,3.1) -- node[above] {$3km$} (1.5,3.1);
        }
        \mpause{
          \draw[<->] (2.1,2.5) -- node[above,sloped] {$8km$} (2.1,.5);
          \draw[gray,dashed] (0,2.5) -- (2.1,2.5);
          \draw[gray,dashed] (1.5,.5) -- (2.1,0.5);
        }
        \mpause{}
        \mpause{
          \node[include=cred] (c) at (1.5,1.5) {};
          \node[anchor=west,xshift=1mm] at (c) {$C$};
        }
        \mpause{
          \draw[ultra thick,cred,<->,shorten <= 0mm, shorten >= 1.2mm] (1.5,2.5) -- node[right] {$x$} (1.5,1.5);
        }
        \node[include=cred] (a) at (0,2.5) {};
        \node[anchor=east,xshift=-1mm] at (a) {$A$};
        \node[include=cred] (b) at (1.5,.5) {};
        \node[anchor=west,xshift=1mm] at (b) {$B$};
      \end{tikzpicture}
    \end{center}
    \end{minipage}~%
    \begin{minipage}{.69\textwidth}
      \pause\pause\pause
      \mpause[1]{
      Introducing notation:
      \begin{itemize}
      \pause\pause
        \item let $C$ be the landing point
      \pause
        \item let $x = $ downstream distance of $A$ to $C$
      \end{itemize}
      \pause
      The time for rowing is and running:\vspace{-1ex}
      \begin{talign}
        t_{\text{row}}(x) &= \mpause[1]{(\sqrt{3^2 + x^2})/6} \\
        \mpause{t_{\text{run}}(x) &=} \mpause{(8-x)/8}
      \end{talign}\vspace{-4ex}
      \pause\pause
      }
    \end{minipage}
    \pause\smallskip
    
    \mpause[1]{
    \pause
    The total time is 
    \quad $t(x) = t_{\text{row}}(x) + t_{\text{run}}(x)$ \quad for $x$ in $[\mpause[1]{0},\mpause[1]{8}]$
    }
    \pause\pause\vspace{-.7ex}
    \begin{talign}
      t'(x) &= \mpause[1]{\frac{x}{6\sqrt{3^2 + x^2}} - \frac{1}{8}} 
      \hspace{1cm} \mpause[8]{t'(x) = 0 \;\iff\; x = 9/\sqrt{7} } 
      \only<-23>{
      \\
      \mpause[2]{t'(x) &= 0 \;\iff\;} 
      \mpause{3\sqrt{3^2 + x^2} = 4x}
      \mpause{\;\stackrel{x\ge 0}{\iff}\; 9(3^2 + x^2) = 16x^2}\\[-.5ex]
      \mpause{&\;\iff\; 7x^2 = 81}
      \mpause{\;\iff\; x^2 = 81/7}
      \mpause{\;\stackrel{x\ge 0}{\iff}\; x = 9/\sqrt{7}}
      }
    \end{talign}
    \pause[25]\vspace{-2ex}%
    
    Now we apply the \pause Closed Interval Method:\vspace{-.5ex}\pause
    \begin{talign}
      t(0) &= \mpause[1]{1.5} &
      t(9/\sqrt{7}) &= \mpause[2]{1 + \sqrt{7}/8 \approx 1.33} &
      t(8) &= \mpause[3]{\sqrt{73}/6 \approx 1.42}
    \end{talign}\vspace{-2.5ex}
    \pause\pause\pause\pause
    
    Thus landing \alert{\mpause[1]{$9/\sqrt{7}$}km downstream} is the fastest. 
  \end{exampleblock}
  \vspace{10cm}
\end{frame}