\begin{frame}
  \frametitle{Optimization}

  \vspace{-1ex}
  \begin{exampleblock}{}
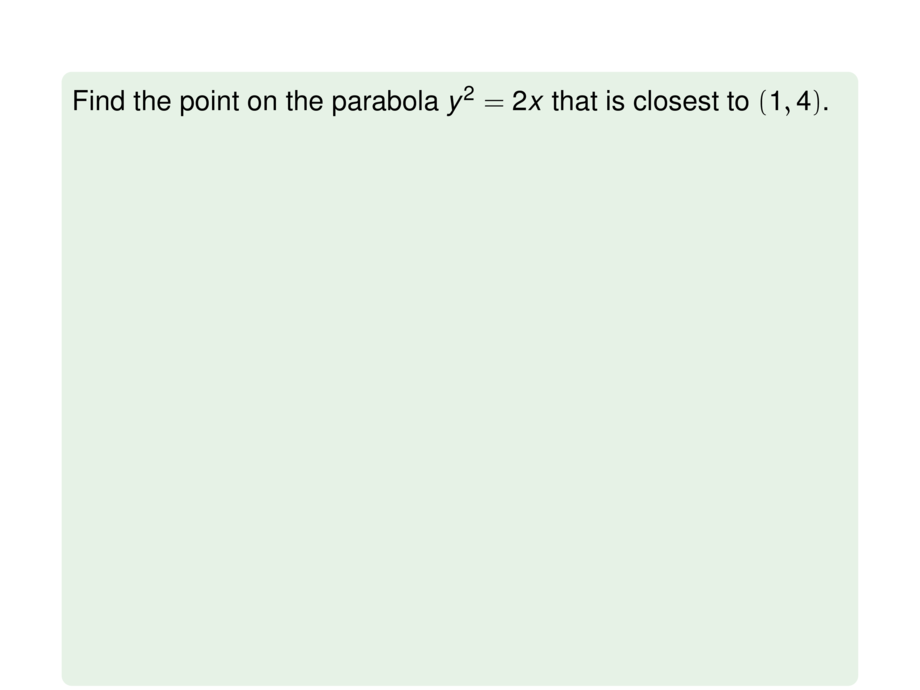
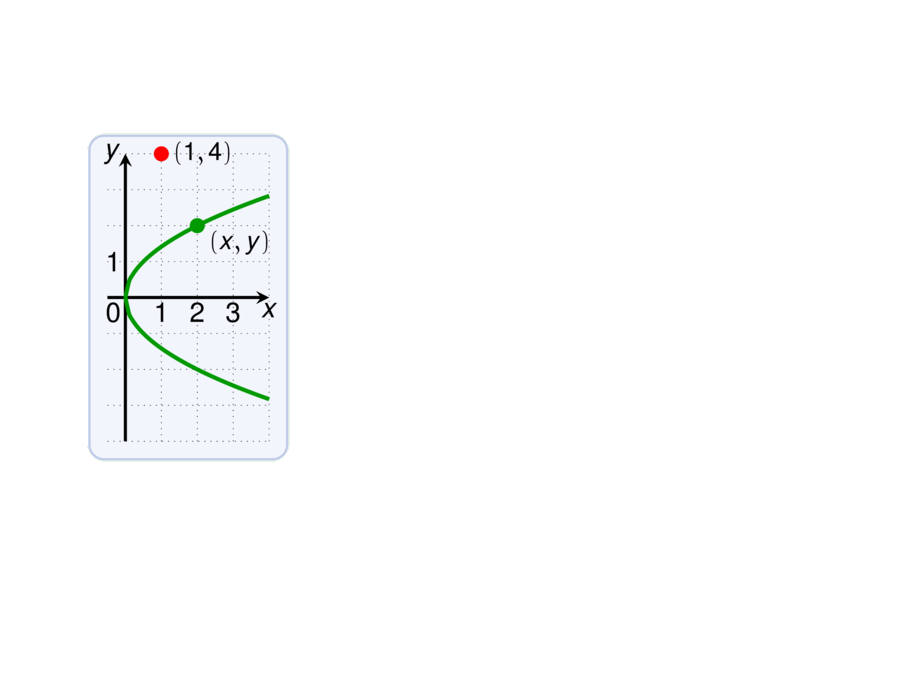
    Find the point on the parabola $y^2 = 2x$ that is closest to $(1,4)$.
    \pause\medskip
    
    \begin{minipage}{.3\textwidth}
    \begin{center}
      \begin{tikzpicture}[default,scale=.5]
        \diagram{-.5}{4}{-4}{4}{1}
        \diagramannotatey{1}
        \diagramannotatex{1,2,3}
        \diagramannotatez
        \begin{scope}[ultra thick]
          \draw[cgreen] plot[smooth,domain=0:4,samples=40] function{sqrt(2*x)};
          \draw[cgreen] plot[smooth,domain=0:4,samples=40] function{-sqrt(2*x)};
        \end{scope}
        \node[include=cred] (a) at (1,4) {};
        \node[anchor=west,xshift=1mm] at (a) {{\small $(1,4)$}};
        \node[include=cgreen] (b) at (2,2) {};
        \node[anchor=north west,xshift=1mm] at (b) {{\small $(x,y)$}};
        \mpause[2]{
        \draw[cred,dashed] (a) -- node[left,yshift=-1mm] {$d$} (b);
        }
      \end{tikzpicture}
    \end{center}
    \end{minipage}
    \begin{minipage}{.69\textwidth}
      \mpause[1]{
      Introducing notation:
      \begin{itemize}
      \pause\pause
        \item let $d$ be the distance of $(x,y)$ to $(1,4)$
      \end{itemize}
      \pause
      Then\vspace{-1ex}
      \begin{talign}
        d &= \mpause[1]{\sqrt{(x-1)^2 + (y-4)^2}} & \mpause{x &=}\mpause{ y^2/2 }
      \end{talign}
      \pause\pause\pause\pause
      Square root makes derivative complicated.\\\pause
      Note that $d$ minimal $\;\iff\;$ \pause $d^2$ minimal.\\\pause
      Thus, instead of $d$ we minimize $d^2$!\vspace{-.5ex}\pause
      \begin{talign}
        f(y) = d^2 = \mpause[1]{(y^2/2-1)^2 + (y-4)^2}
      \end{talign}\vspace{-3ex}
      }
    \end{minipage}
    \pause\mpause[1]{\pause
    \begin{talign}
      &f'(y) = \mpause[1]{2(y^2/2-1)y + 2(y-4)} \mpause{= y^3-8} \\
      &\mpause{f'(y) = 0 \;\iff\;} \mpause{y = 2}
    \end{talign}
    \pause\pause\pause\pause\pause
    Moreover $f'(y) < 0$ for all $y < 2$ and  $f'(y) > 0$ for all $y > 2$.
    \pause\smallskip
    
    Thus by the First Derivative Test for Absolute Extrema,
    $f(2)$ is the absolute minimum.
    \pause
    Thus the point \alert{$(\mpause[1]{2},\mpause[1]{2})$ is closest to $(1,4)$}.
    }
  \end{exampleblock}
  \vspace{10cm}
\end{frame}