





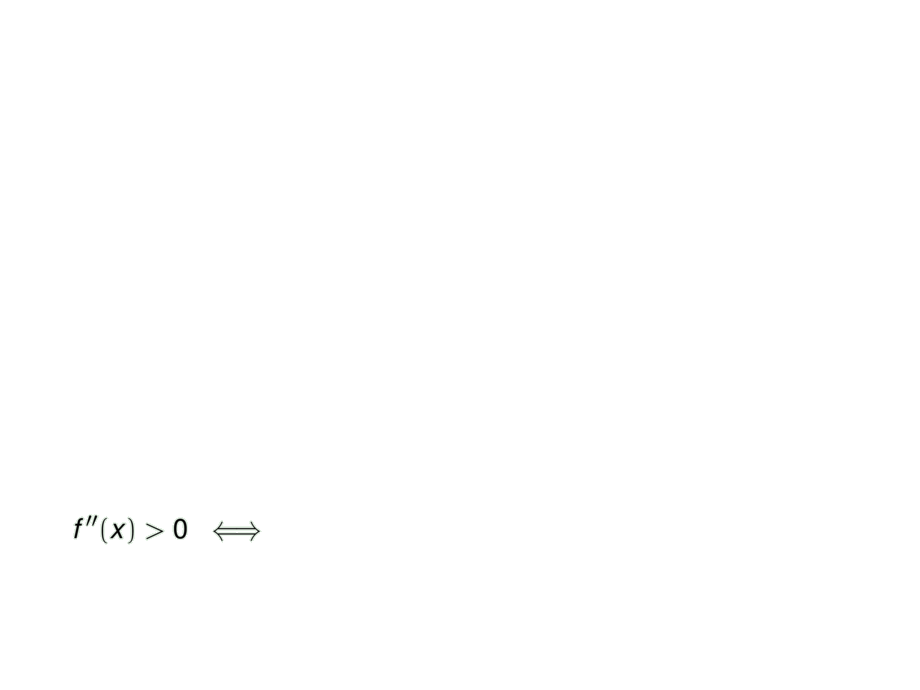

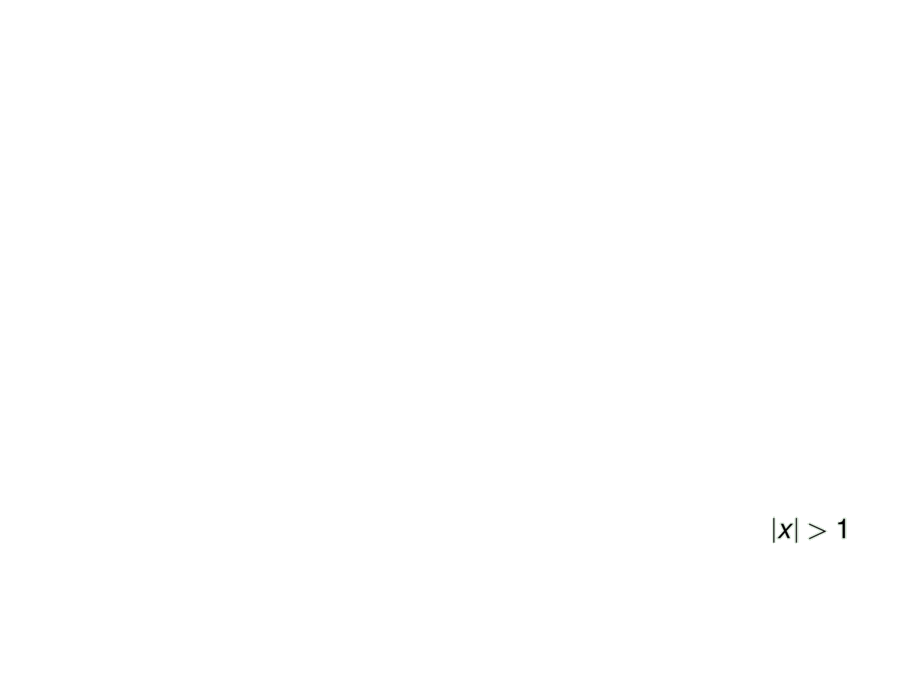


























































































61/121
\begin{frame}
\frametitle{Curve Sketching}
\begin{exampleblock}{}
Sketch the curve of $f(x) = \frac{2x^2}{x^2-1}$.
\pause\bigskip
\only<-18>{
The domain is \pause $\{x \mid x \ne \pm 1\}$\pause , that is, $(-\infty,-1) \cup (-1,1) \cup (1,\infty)$
\pause\bigskip
We have \quad $f(0) = \pause 0$ \pause\quad and \quad $f(x) = 0 \;\iff\;\pause x = 0$
\pause\bigskip
The vertical asymptotes are \pause\quad $x = -1$ \quad and \quad $x = 1$
\begin{talign}
\lim_{x \to -1^-} = \mpause[1]{\infty}
&& \lim_{x \to -1^+} = \mpause[2]{-\infty}
&& \lim_{x \to 1^-} = \mpause[3]{-\infty}
&& \lim_{x \to 1^+} = \mpause[4]{\infty}
\end{talign}
\pause\pause\pause\pause\pause
The horizontal asymptotes are \mpause[3]{ \quad $y = 2$}
\begin{talign}
\lim_{x \to \infty} f(x) = \mpause[1]{2}
&& \lim_{x \to -\infty} f(x) = \mpause[2]{2}
\end{talign}
\pause\pause\pause\pause
}
\only<19-30>{
\pause[19]
The derivative is:
\begin{talign}
f'(x) = \mpause[1]{ \frac{4x(x^2-1) - 2x^2(2x)}{(x^2-1)^2} }
\mpause[2]{= \frac{-4x}{(x^2-1)^2} }
\end{talign}
\pause\pause\pause
Thus
\begin{itemize}
\item increasing ($f'(x) > 0$) on \pause $(-\infty,-1)\cup (-1,0)$
\pause
\item decreasing on ($f'(x) < 0$) on \pause $(0,1)\cup (1,\infty)$
\end{itemize}
\pause\bigskip
The critical numbers are \pause\quad $x = 0$ \quad (since $f'(0) = 0$)
\pause
\begin{itemize}
\item $f'(x)$ \pause changes from $+$ to $-$ at $0$ $\;\implies\;$ \pause local maximum $(0,0)$
\end{itemize}
\pause
}
\only<31->{
\pause[31]\vspace{-2ex}
\begin{talign}
f'(x) = \frac{-4x}{(x^2-1)^2}
\end{talign}
The second derivative is:
\begin{talign}
f''(x)
&= \mpause[1]{ \frac{-4(x^2-1)^2 - (-4x)\cdot 2(x^2-1)\cdot 2x}{(x^2-1)^4} } \\
&\mpause[2]{= \frac{-4(x^2-1) + 16x^2}{(x^2-1)^3} }
\mpause[3]{= \frac{12x^2 + 4}{(x^2-1)^3} }
\end{talign}\vspace{-2ex}
\pause\pause\pause\pause
\begin{talign}
&12x^2 + 4 > 0 \quad \text{for all $x$} \\
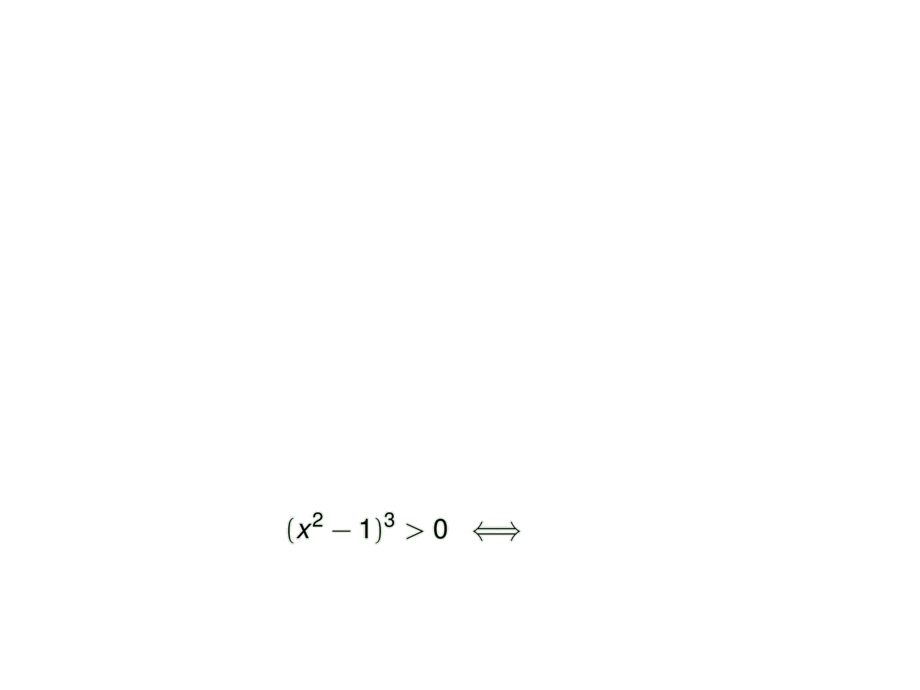
&\mpause[1]{f''(x) > 0 \;\iff\; } \mpause[2]{(x^2-1)^3 > 0 \;\iff\; }
\mpause[3]{x^2-1 > 0 \;\iff\; }
\mpause[4]{|x| > 1} %\\
% &\mpause[5]{f''(x) < 0 \;\iff\; }
% \mpause[6]{|x| < 1}
\end{talign}\vspace{-3ex}
\pause\pause\pause\pause\pause%\pause\pause
\begin{itemize}
\item concave upward on \pause $(-\infty,-1)\cup (1,\infty)$
\pause
\item concave downward on \pause $(-1,1)$
\pause
\item inflection points: \pause none ($-1$ and $1$ not in the domain)
\end{itemize}
}
\end{exampleblock}
\vspace{10cm}
\end{frame}

