










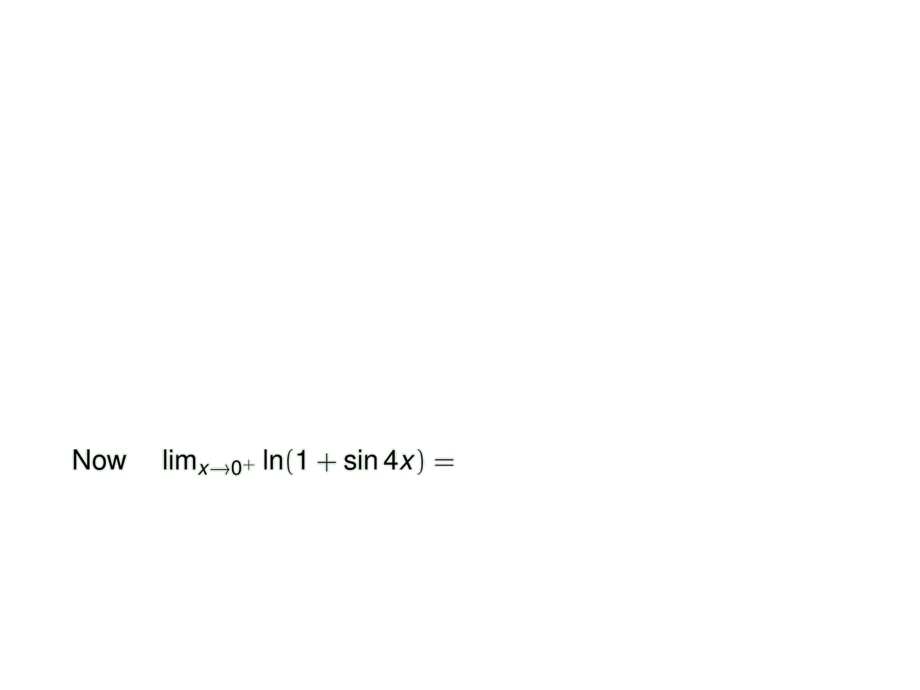
























































































117/118
\begin{frame}
\frametitle{L'Hospital's Rule}
\begin{exampleblock}{}
Evaluate the limit\vspace{-3ex}
\begin{talign}
\lim_{x\to 0^+} (1 + \sin 4x)^{\cot x}
\end{talign}
\pause
Then
\quad $\lim_{x\to 0^+} (1 +\sin 4x) = \pause 1$ \pause\quad and \quad $\lim_{x\to 0^+} \cot x = \pause \infty$
\pause\medskip
We write the limit as:
\begin{talign}
\lim_{x\to 0^+} (1 + \sin 4x)^{cot x}
&\mpause[1]{ = \lim_{x\to 0^+} e^{\ln (1 + \sin 4x)^{cot x}} } \\
&\mpause[2]{ = e^{\lim_{x\to 0^+} \left( \cot x \cdot \ln (1 + \sin 4x) \right) } } \\
\mpause[3]{\lim_{x\to 0^+} \left( \cot x \cdot \ln (1 + \sin 4x) \right)}
&\mpause[4]{= \lim_{x\to 0^+} \frac{\ln (1 + \sin 4x)}{\tan x}}
\end{talign}
\pause\pause\pause\pause\pause
Now
\quad $\lim_{x\to 0^+} \ln (1 + \sin 4x) = \pause 0$ \pause\quad and \quad $\lim_{x\to 0^+} \tan x = \pause 0$
\pause\medskip
Hence we can apply l'Hospital's Rule:
\begin{talign}
\lim_{x\to 0^+} \frac{\ln (1 + \sin 4x)}{\tan x}
&\mpause[1]{ = \lim_{x\to 0^+} \frac{\frac{4\cos 4x}{1 + \sin 4x}}{(\sec x)^2} }
\mpause[2]{ = \frac{\left(\frac{4}{1}\right)}{1}}
\mpause[3]{ = 4}
\end{talign}
\pause\pause\pause\pause
Thus \quad $\lim_{x\to 0^+} (1 + \sin 4x)^{\cot x} = e^4$
\end{exampleblock}
\end{frame}

