


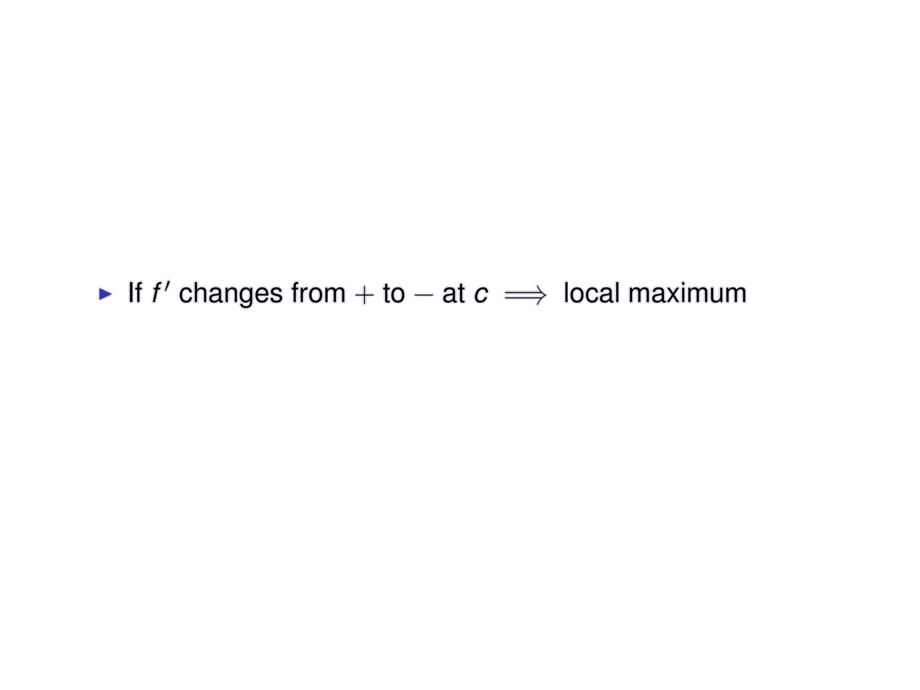
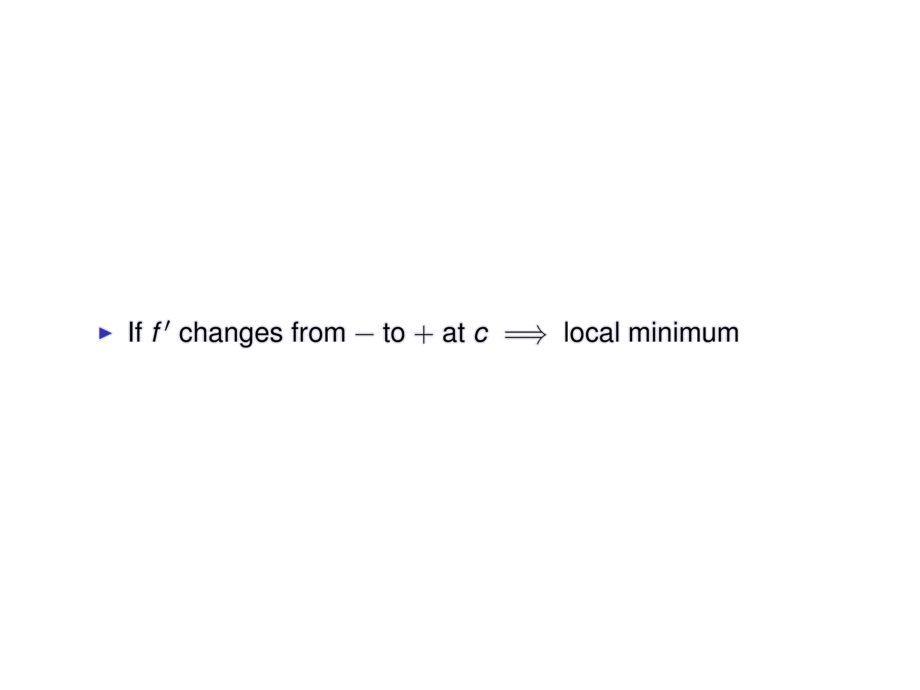






























































































157/158
\begin{frame}
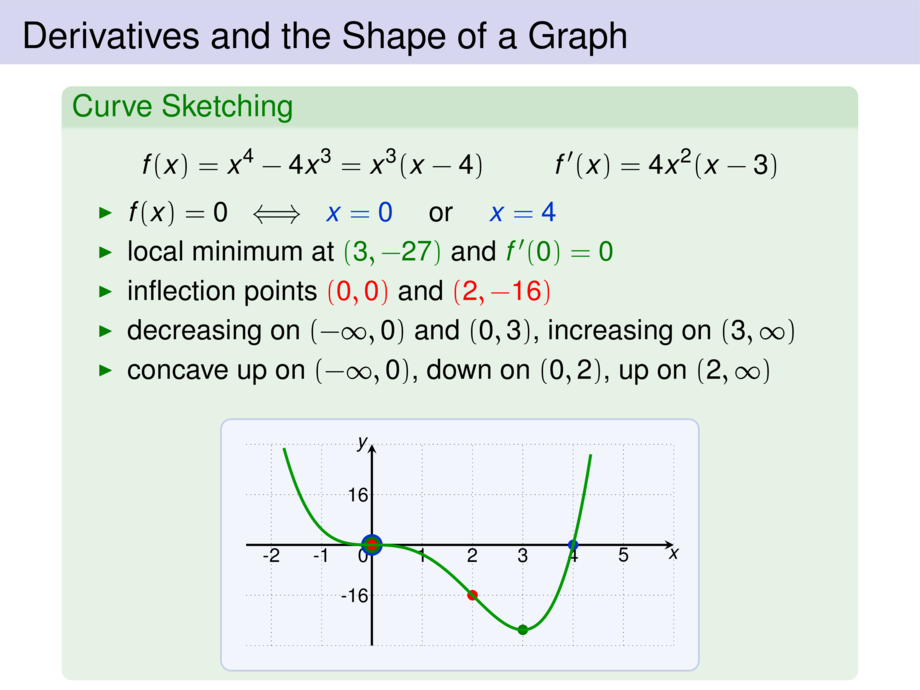
\frametitle{Derivatives and the Shape of a Graph}
\begin{block}{Summary: Finding Local Extrema}
\pause
Find critical numbers $c$: $f'(c) = 0$ or $f'(c)$ does not exist.
\pause\medskip
First \emph{Derivative Test} ($f$ needs to be continuous at $c$):
\begin{itemize}
\pause
\item If $f'$ changes from $+$ to $-$ at $c$ $\implies$ local maximum
\pause
\item If $f'$ changes from $-$ to $+$ at $c$ $\implies$ local minimum
\pause
\item If $f'$ does not change sign at $c$ $\implies$ no local extremum
\end{itemize}
\pause\medskip
The \emph{Second Derivative Test}:
\begin{enumerate}
\pause
\item $f'(c) = 0$ and $f''(c) > 0$ $\implies$ local minimum
\pause
\item $f'(c) = 0$ and $f''(c) < 0$ $\implies$ local maximum
\pause
\item $f'(c)$ or $f''(c)$ does not exist or $f''(c) = 0$\\ $\implies$ use the First Derivative Test
\end{enumerate}
\end{block}
\end{frame}

