


































































































148/158
\begin{frame}
\frametitle{Derivatives and the Shape of a Graph}
\begin{exampleblock}{Curve Sketching}
\begin{malign}
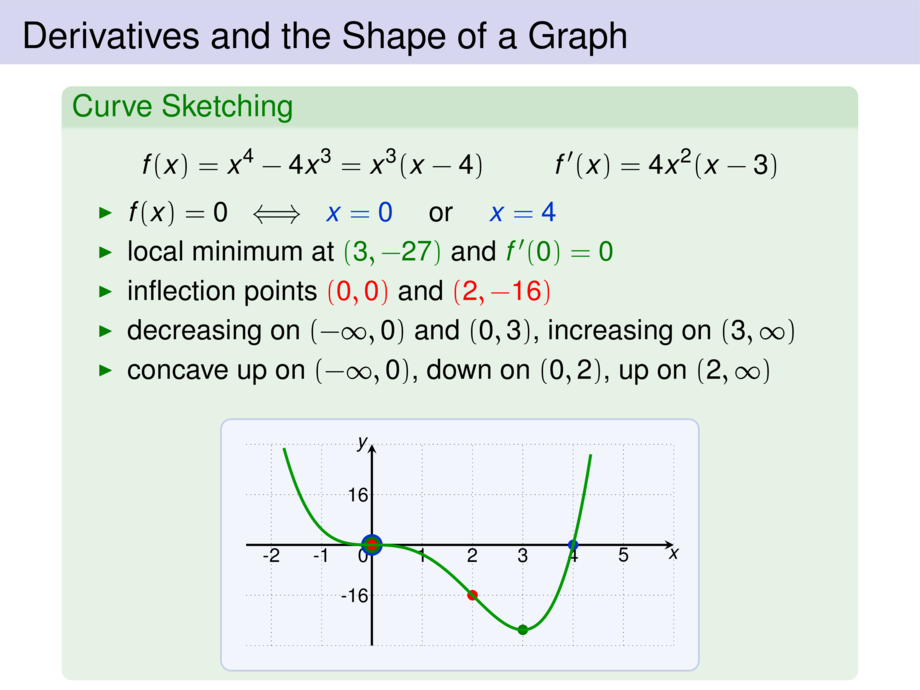
f(x) = x^4 - 4x^3 = x^3 (x - 4)
&& f'(x) &= 4x^2(x - 3)
\end{malign}\vspace{-1ex}
\begin{itemize}
\pause
\item $f(x) = 0 \;\iff\;$ \pause \textcolor{cblue}{$x = 0$} \quad or \quad \textcolor{cblue}{$x = 4$}
\pause
\item local minimum at \textcolor{cdgreen}{$(3,-27)$} and \textcolor{cdgreen}{$f'(0) = 0$}
\pause
\item inflection points \textcolor{cred}{$(0,0)$} and \textcolor{cred}{$(2,-16)$}
\pause
\item decreasing on \pause $(-\infty,0)$ and $(0,3)$, \pause increasing on \pause $(3,\infty)$
\pause
\item concave up on $(-\infty,0)$, down on $(0,2)$, up on $(2,\infty)$
\end{itemize}
\pause[1]
\begin{center}
\scalebox{.7}{
\begin{tikzpicture}[default,baseline=1cm]
\diagram{-2.5}{6}{-2}{2}{1}
\diagramannotatez
\diagramannotatex{-2,-1,1,2,3,4,5}
\diagramannotateyy{-1/-16,1/16}
\mpause[2]{
\node[include=cblue,minimum size=4mm] at (0,0) {};
\node[include=cblue] at (4,0) {};
}
\mpause[3]{
\node[include=cdgreen] at (3,-27/16) {};
\node[include=cdgreen,minimum size=3mm] at (0,0) {};
}
\mpause[4]{
\node[include=cred] at (0,0) {};
\node[include=cred] at (2,-16/16) {};
}
\begin{scope}[ultra thick]
\mpause[10]{
\draw[cgreen] plot[smooth,domain=-1.75:0,samples=30] function{(x**4 - 4*x**3)/16};
}
\mpause[11]{
\draw[cgreen] plot[smooth,domain=-0:2,samples=30] function{(x**4 - 4*x**3)/16};
}
\mpause[12]{
\draw[cgreen] plot[smooth,domain=2:3,samples=30] function{(x**4 - 4*x**3)/16};
}
\mpause[13]{
\draw[cgreen] plot[smooth,domain=3:4.35,samples=30] function{(x**4 - 4*x**3)/16};
}
\end{scope}
\end{tikzpicture}
}
\end{center}
\end{exampleblock}
\end{frame}

