\begin{frame}
  \frametitle{Derivatives and the Shape of a Graph}

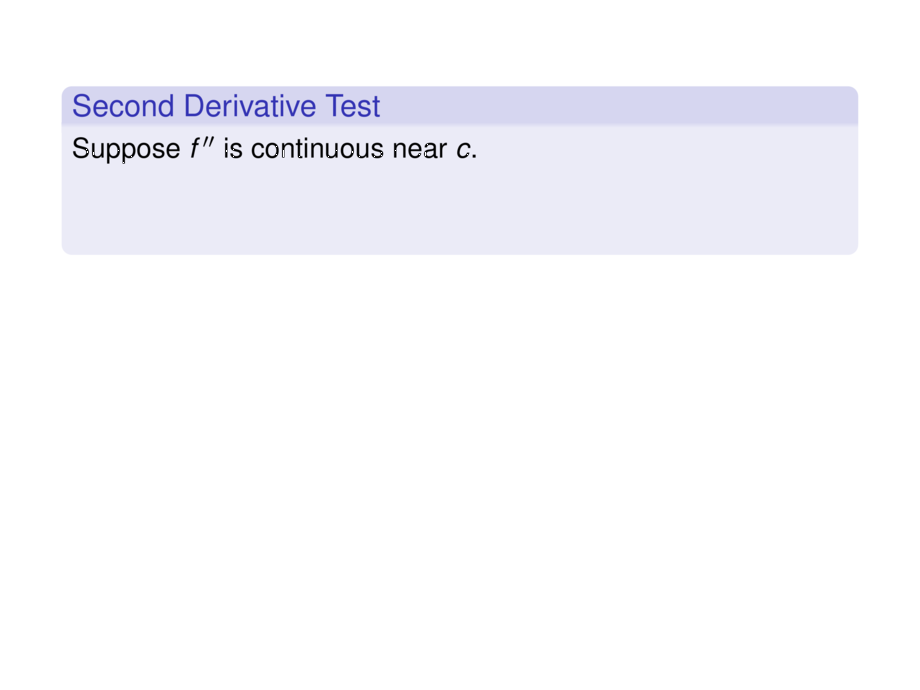
  \begin{block}{Second Derivative Test}
    Suppose $f''$ is continuous near $c$.
    \begin{itemize}
    \pause
      \item If $f'(c) = 0$ and $f''(c) > 0$, then $f$ has a local minimum at $c$.
    \pause
      \item If $f'(c) = 0$ and $f''(c) <0$, then $f$ has a local maximum at $c$.
    \end{itemize}
  \end{block}
  \pause

  \begin{exampleblock}{}
    Where does $f(x) = x^4 - 4x^3$ have local extrema?\vspace{-.6ex}
    \pause
    \begin{talign}
      f'(x) &= 4x^3 - 12x^2 \mpause[1]{= 4x^2(x - 3)} \\
      f''(x) &= 12x^2 - 24x = 12x(x - 2)
    \end{talign}
    \pause\pause
    Thus $f'(x) = 0$ for \alert{$x = \mpause[1]{0}$} and \alert{$x = \mpause[1]{3}$}.
%     These are the only critical numbers as $f'$ is defined everywhere.
    \pause\pause
    Second Derivative Test:\vspace{-.6ex}
    \begin{talign}
      f''(0) &= \mpause[1]{0} &
      \mpause[2]{f''(3) &= } \mpause[3]{36} \mpause[4]{> 0}
    \end{talign}
    \pause\pause\pause\pause\pause
    Thus $f(3) = -27$ is a local minimum as $f'(3) = 0$ and $f''(3) > 0$.\\
    \pause\medskip
    
    The Second Derivative Test gives \alert{no information for $f''(0) = 0$}.\\
    \pause\medskip
        
    However, the First Derivative Test \ldots \pause
    yields that \alert{$f(0) = 0$ is no extremum}
    since $f'(x) < 0$ for $x < 0$ and $0 < x < 3$. 
  \end{exampleblock}  
\end{frame}