



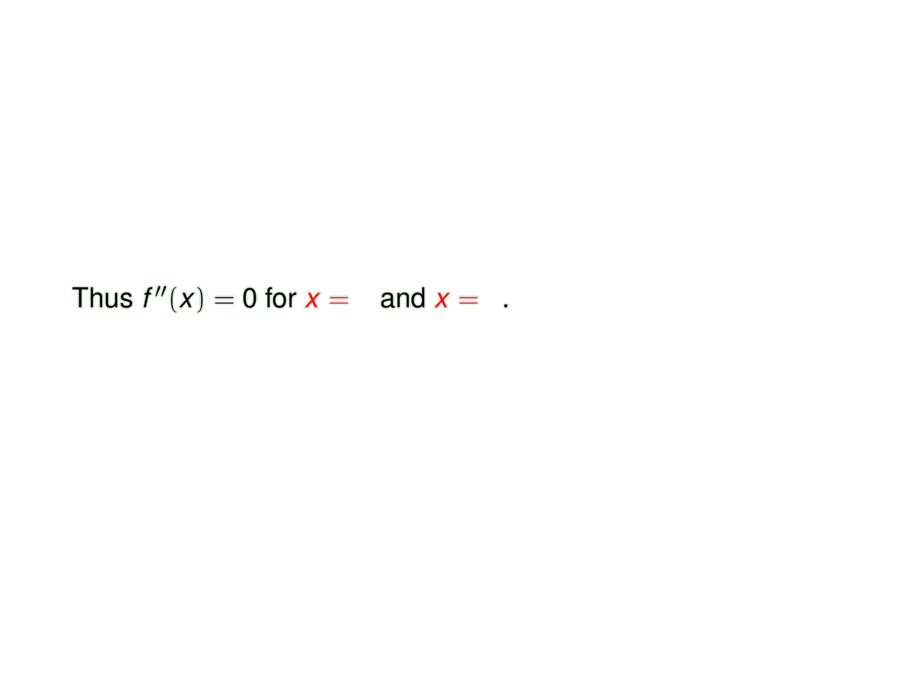
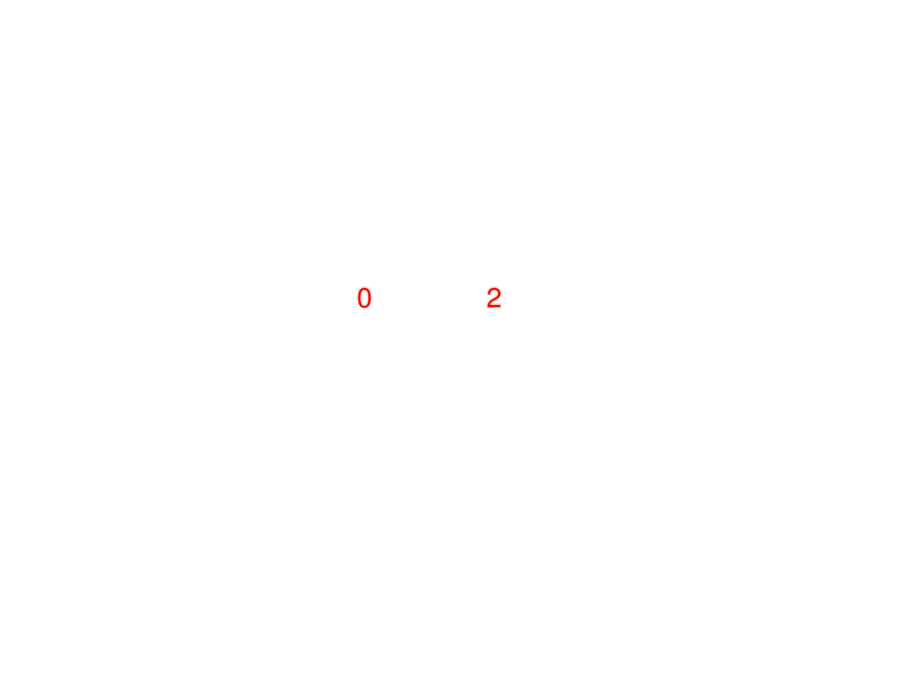
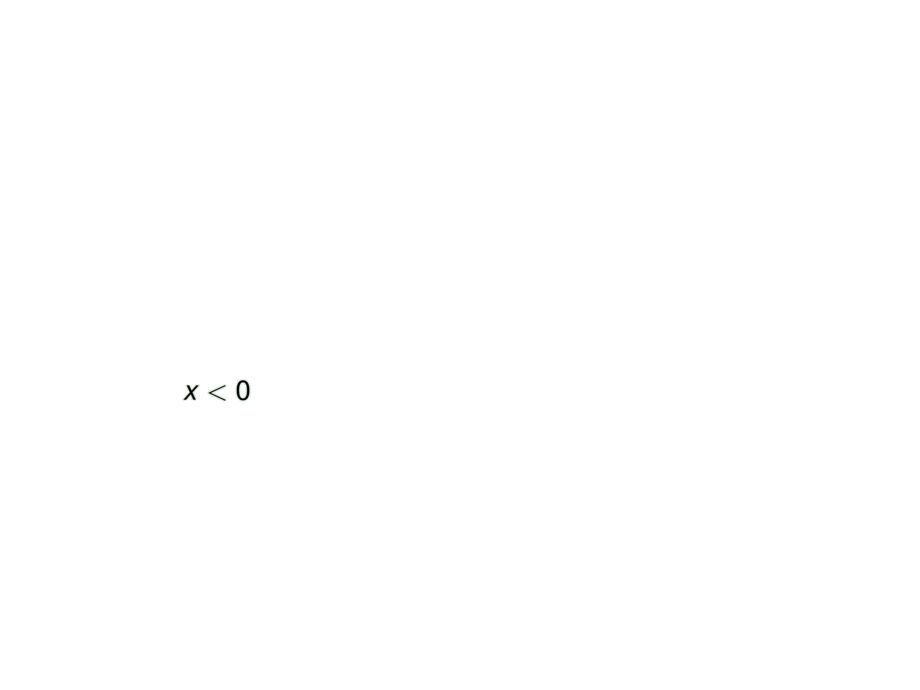

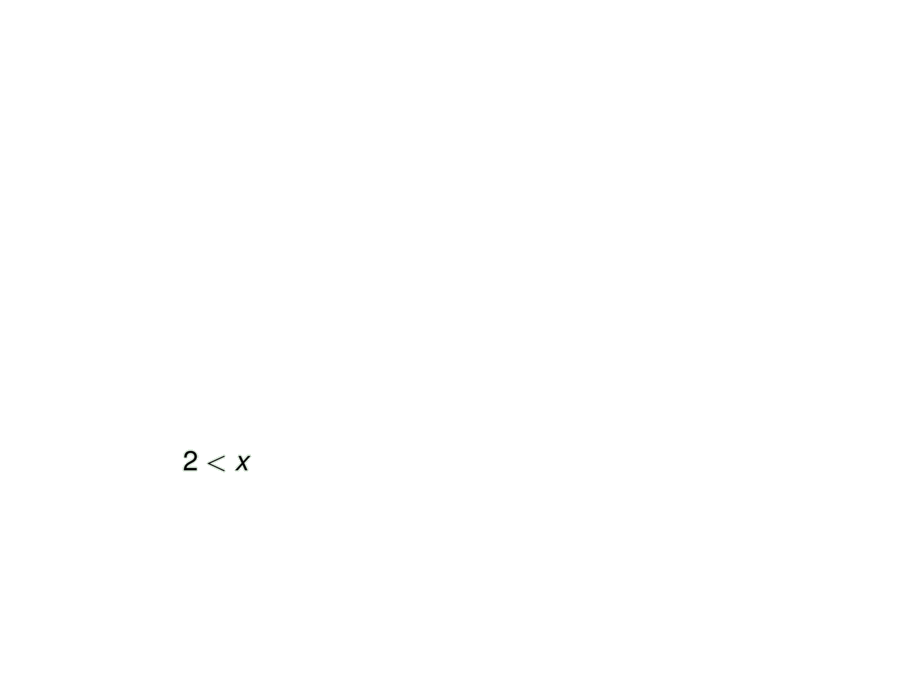

























































































116/158
\begin{frame}
\frametitle{Derivatives and the Shape of a Graph}
\begin{exampleblock}{}
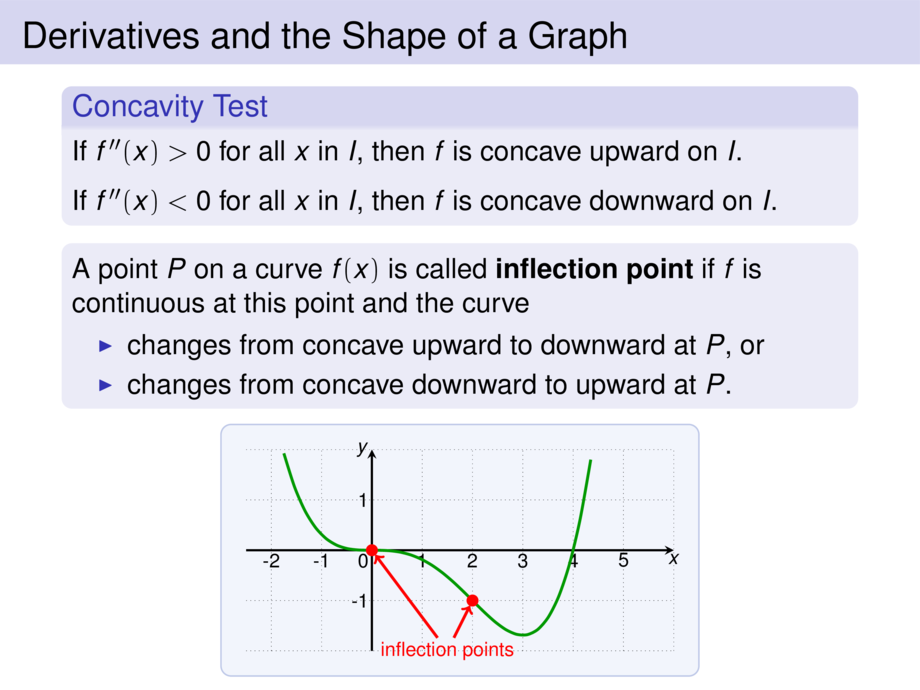
Where are inflection points of $f(x) = x^4 - 4x^3$?
\pause
\begin{talign}
f'(x) &= 4x^3 - 12x^2 \\
\mpause[1]{f''(x) &= 12x^2 - 24x} \mpause[2]{= 12x(x - 2)}
\end{talign}
\pause\pause\pause
Thus $f''(x) = 0$ for \alert{$x = \mpause[1]{0}$} and \alert{$x = \mpause[1]{2}$}.
\begin{center}
\pause\pause
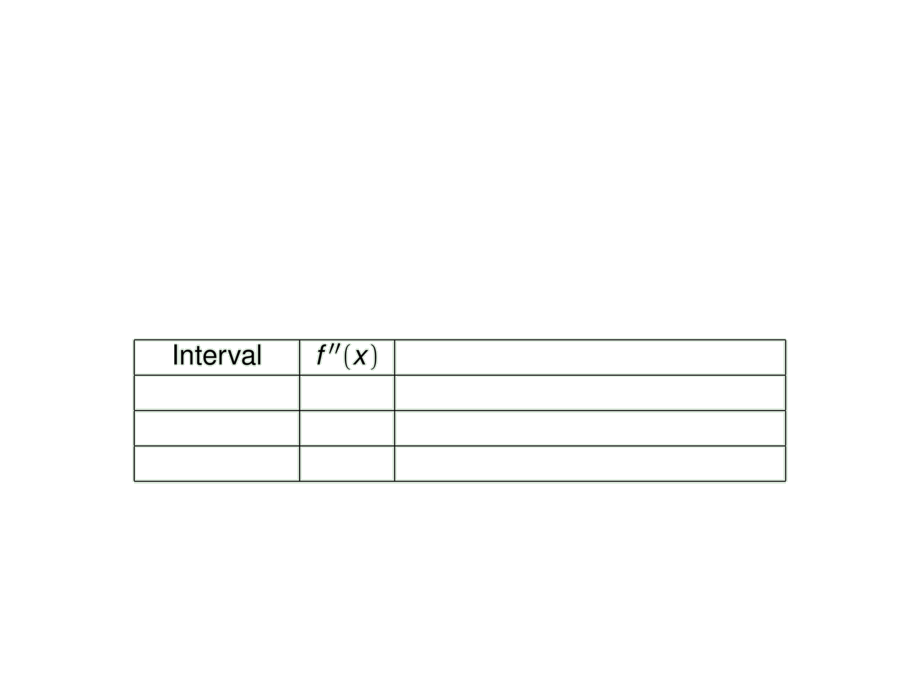
\begin{tabular}{|c|c|l|}
\hline
Interval & $f''(x)$ & \\
\hline
\mpause[1]{ $x < 0$ } & \mpause[4]{+} & \mpause{ concave upward on $(-\infty,0)$ } \\
\hline
\mpause[2]{ $0 < x < 2$ } & \mpause[6]{-} & \mpause{ concave downward on $(0,2)$ } \\
\hline
\mpause[3]{ $2 < x$ } & \mpause[8]{+} & \mpause{ concave upward on $(2,\infty)$ } \\
\hline
\end{tabular}
\end{center}
\pause\pause\pause\pause\pause\pause\pause\pause\pause\pause
Thus the \alert{inflection points} are:
\begin{itemize}
\pause
\item \alert{$(0,0)$} since the curve changes from concave up to down
\pause
\item \alert{$(2,-16)$} since the curve changes from concave down to up
\end{itemize}
\end{exampleblock}
\end{frame}

