\begin{frame}
  \frametitle{Derivatives and the Shape of a Graph}

  \begin{block}{Concavity Test}
    If $f''(x) > 0$ for all $x$ in $I$, then $f$ is concave upward on $I$.
    \pause\medskip
    
    If $f''(x) < 0$ for all $x$ in $I$, then $f$ is concave downward on $I$.
  \end{block}
  \pause
  
  \begin{block}{}
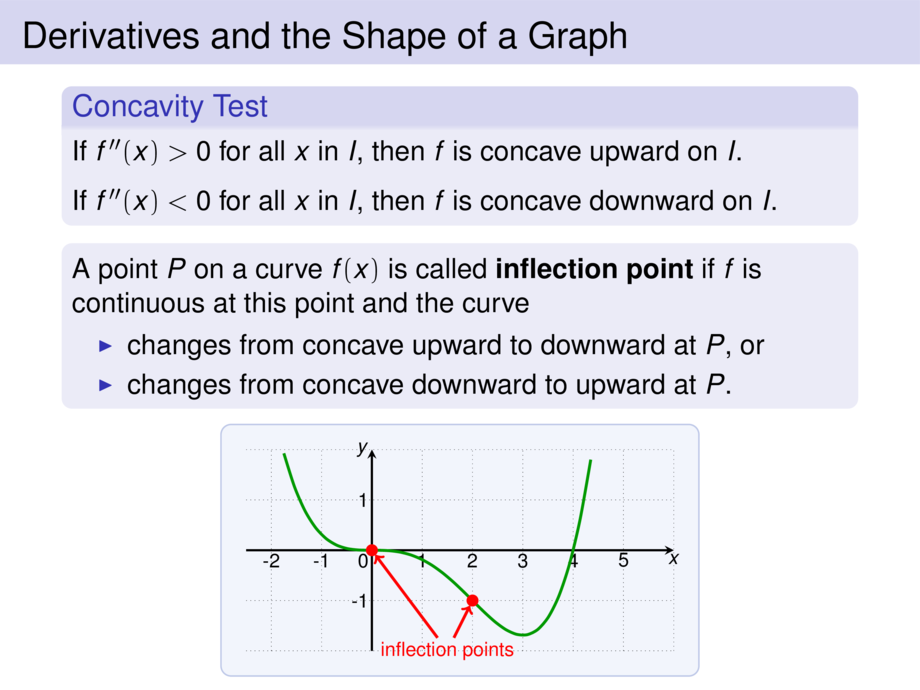
    A point $P$ on a curve $f(x)$ is called \emph{inflection point}
    if $f$ is continuous at this point and the curve 
    \begin{itemize}
      \item changes from concave upward to downward at $P$, or
      \item changes from concave downward to upward at $P$.
    \end{itemize} 
  \end{block}
  \pause
  
  \begin{center}
    \scalebox{.7}{
    \begin{tikzpicture}[default,baseline=1cm]
      \diagram{-2.5}{6}{-2}{2}{1}
      \diagramannotatez
      \diagramannotatex{-2,-1,1,2,3,4,5}
      \diagramannotatey{-1,1}
      \begin{scope}[ultra thick]
        \draw[cgreen] plot[smooth,domain=-1.75:4.35,samples=30] function{(x**4 - 4*x**3)/16};
      \end{scope}
      \mpause[1]{
      \begin{scope}[cred,ultra thick]
        \node[include=cred] (na) at (0,0) {};
        \node[include=cred] (nb) at (2,-16/16) {};
        \node (i) at (1.5,-2) {inflection points};
        \draw[->] (i) -- (na);
        \draw[->] (i) -- (nb);
      \end{scope}
      }
    \end{tikzpicture}
    }
  \end{center}
\end{frame}