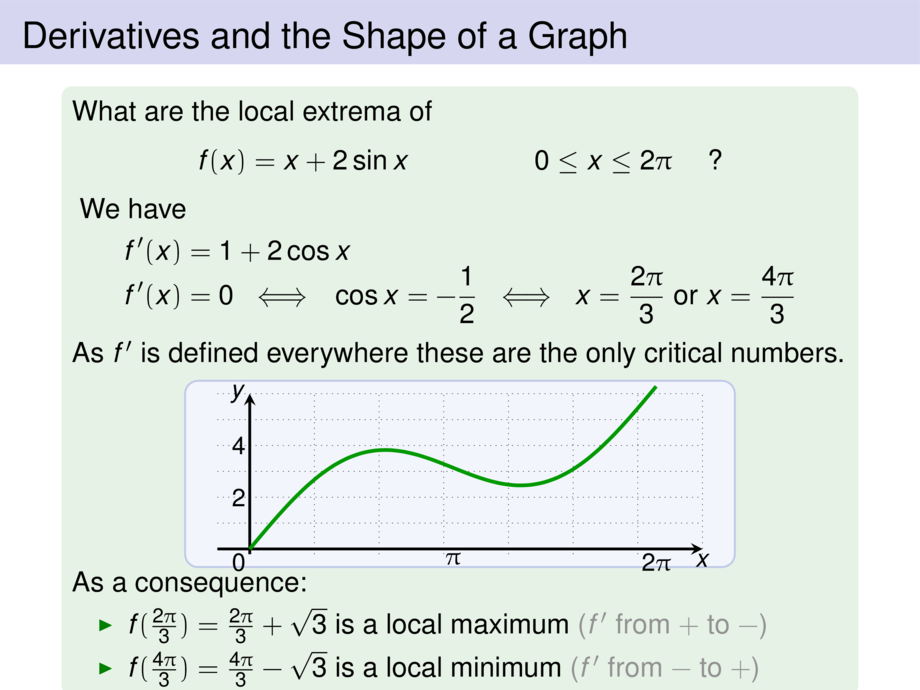


































































































74/158
\begin{frame}
\frametitle{Derivatives and the Shape of a Graph}
\begin{block}{}
Let $I$ be an interval. If the graph of $f$ is called
\begin{itemize}
\pause
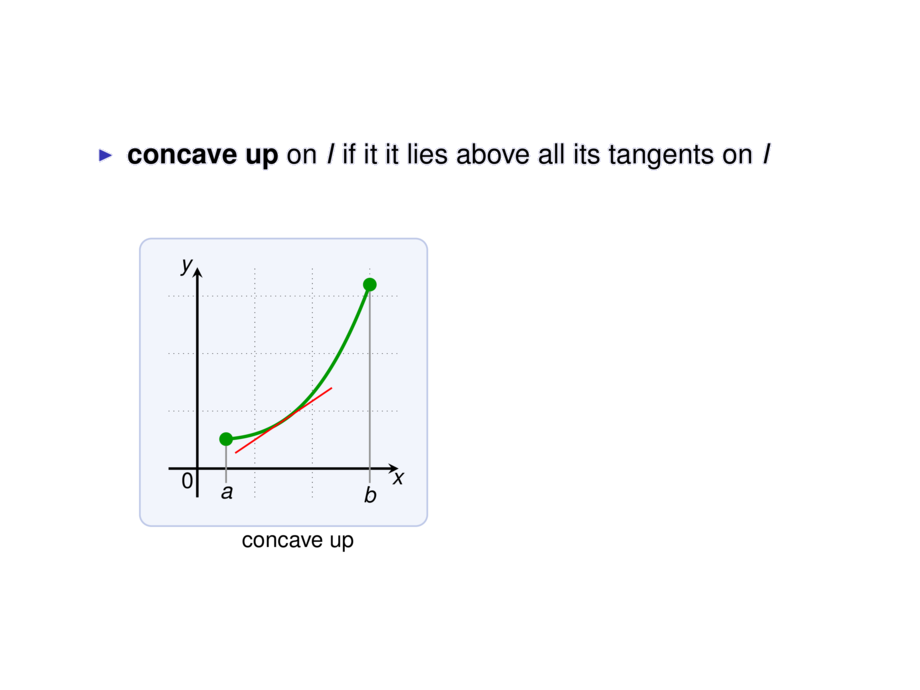
\item \emph{concave up} on $I$ if it it lies above all its tangents on $I$
\pause
\item \emph{concave down} on $I$ if it it lies below all its tangents on $I$
\end{itemize}
\end{block}
\pause[1]\medskip
\begin{center}\vspace{-1ex}
\scalebox{.8}{
\pause
\begin{tikzpicture}[default,baseline=1cm]
\diagram{-.5}{3.5}{-.5}{3.5}{1}
\diagramannotatez
\begin{scope}[ultra thick]
\draw[cgreen] plot[smooth,domain=.5:3,samples=30] function{.5+x**3/10};
\node[include=cgreen] (na) at (.5,.5+.5^3/10) {};
\node[include=cgreen] (nb) at (3,.5+3^3/10) {};
\end{scope}
\draw[gray] (na) -- node[at end, below,black] {$a$} (.5,-.25);
\draw[gray] (nb) -- node[at end,below,black] {$b$} (3,-.25);
\tangent{1cm}{1cm}{.5+pow(\x,3)/10}{1.5}
\node at (1.75,-1.3) {concave up};
\end{tikzpicture}\hspace{1cm}
\pause
\begin{tikzpicture}[default,baseline=1cm]
\diagram{-.5}{3.5}{-.5}{3.5}{1}
\diagramannotatez
\begin{scope}[ultra thick]
\draw[cgreen] plot[smooth,domain=.5:3,samples=30] function{3.2-(3.5-x)**3/10};
\node[include=cgreen] (na) at (.5,.5+.5^3/10) {};
\node[include=cgreen] (nb) at (3,.5+3^3/10) {};
\end{scope}
\draw[gray] (na) -- node[at end, below,black] {$a$} (.5,-.25);
\draw[gray] (nb) -- node[at end,below,black] {$b$} (3,-.25);
\tangent{1cm}{1cm}{3.2-pow(3.5-\x,3)/10}{2}
\node at (1.75,-1.3) {concave down};
\end{tikzpicture}
}
\end{center}
\mpause[1]{
Imagine the graph as a street \& a car driving from left to right:
\begin{itemize}
\pause\pause
\item then concave upward = turning left \pause (increasing slope)
\pause
\item then concave downward = turning right \pause (decreasing slope)
\end{itemize}
}
\end{frame}

