


































































































50/158
\begin{frame}
\frametitle{Derivatives and the Shape of a Graph}
\begin{exampleblock}{}
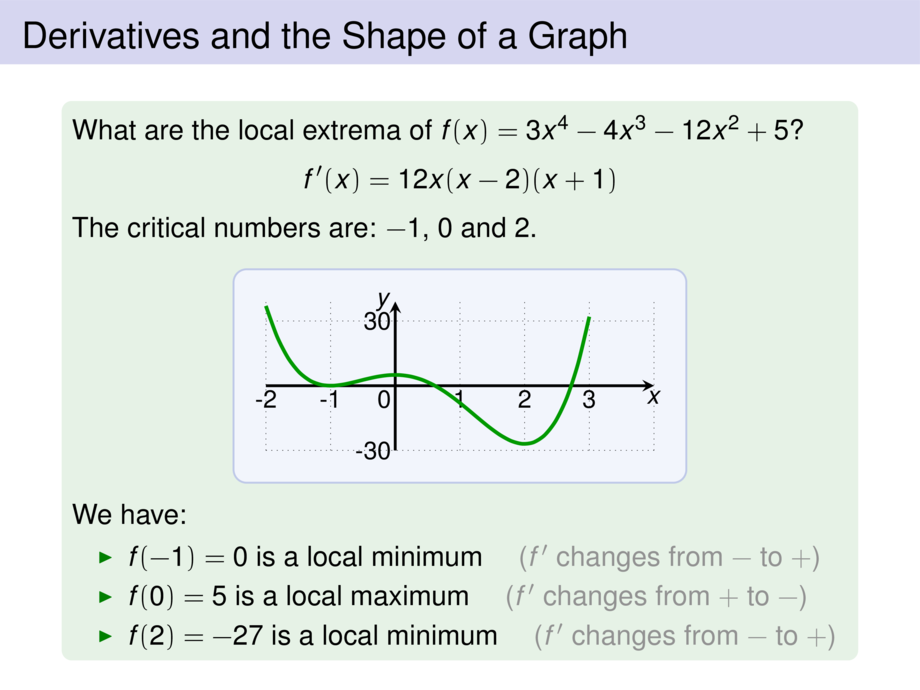
What are the local extrema of $f(x) = 3x^4 - 4x^3 -12x^2 + 5$?
\begin{talign}
f'(x) = 12x(x-2)(x+1)
\end{talign}
\pause
The critical numbers are: \pause $-1$, $0$ and $2$.
\pause\medskip
\begin{overlayarea}{\textwidth}{3cm}
\only<-10>{
We have already seen that:\smallskip
{\small
\begin{tabular}{|c|c|c|c|c|l|}
\hline
Interval & $12x$ & $x-2$ & $x+1$ & $f'(x)$ & \\
\hline
x < -1 & - & - & - & - & decreasing on $(-\infty,-1)$ \\
\hline
-1 < x < 0 & - & - & + & + & increasing on $(-1,0)$ \\
\hline
0 < x < 2 & + & - & + & - & decreasing on $(0,2)$ \\
\hline
2 < x & + & + & + & + & increasing on $(2,\infty)$ \\
\hline
\end{tabular}
}
}
\only<11>{
\begin{center}\vspace{-1ex}
\scalebox{.9}{
\begin{tikzpicture}[default,baseline=1cm]
\diagram{-2}{4}{-1}{1.3}{1}
\diagramannotatez
\diagramannotateyy{-1/-30,1/30}
\diagramannotatex{-2,-1,1,2,3}
\begin{scope}[ultra thick]
\draw[cgreen] plot[smooth,domain=-2:3,samples=30] function{(3*x**4 - 4*x**3 - 12*x**2 + 5)/30};
\end{scope}
\end{tikzpicture}\vspace{-1ex}
}
\end{center}
}
\end{overlayarea}
\pause\medskip
We have:
\begin{itemize}
\item $f(-1) = 0$ is \pause a local minimum \quad\textcolor{gray}{($f'$ changes from $-$ to $+$)}
\pause
\item $f(0) = 5$ is \pause a local maximum \quad\textcolor{gray}{($f'$ changes from $+$ to $-$)}
\pause
\item $f(2) = -27$ is \pause a local minimum \quad\textcolor{gray}{($f'$ changes from $-$ to $+$)}
\end{itemize}
\end{exampleblock}
\end{frame}

