\begin{frame}
  \frametitle{Derivatives and the Shape of a Graph}

  \begin{block}{First Derivative Test}
    Suppose that $c$ is a critical number of a continuous function $f$.\\
    \begin{itemize}
    \pause
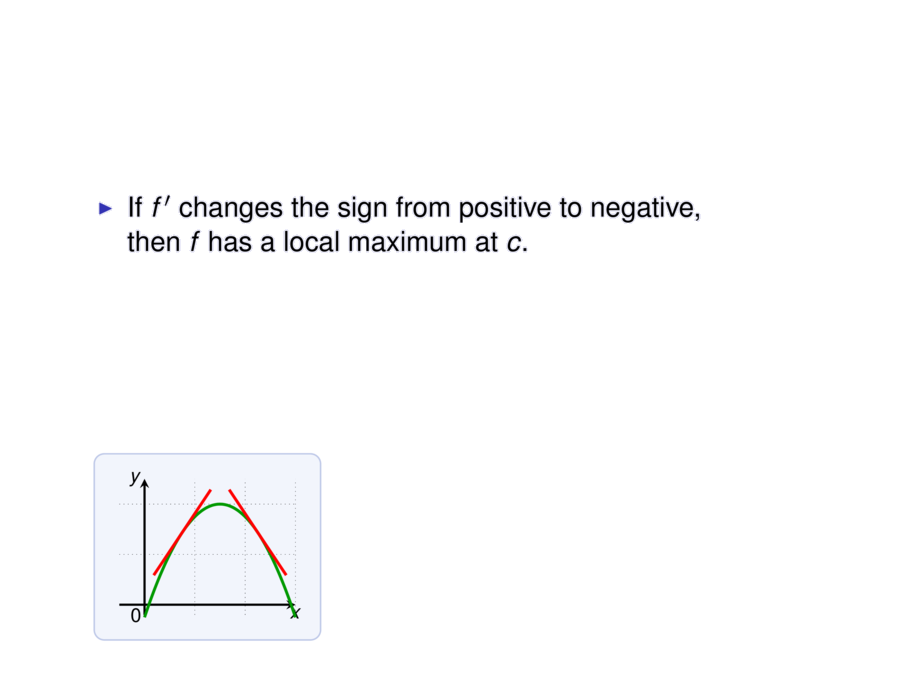
      \item If $f'$ changes the sign from positive to negative,\\
        then $f$ has a local maximum at $c$.
    \pause\smallskip
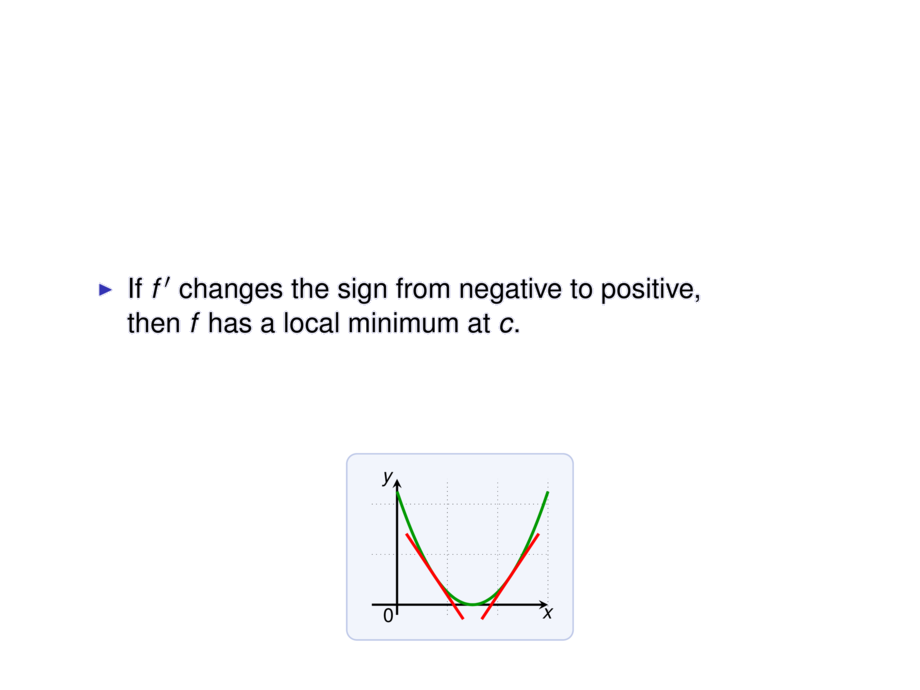
      \item If $f'$ changes the sign from negative to positive,\\
        then $f$ has a local minimum at $c$.
    \pause\smallskip
      \item If $f'$ does not change sign at $c$,\\
        then $f$ has no local extremum at $c$.
    \end{itemize}
  \end{block}
  \pause[1]
  
  \begin{center}
  \scalebox{.7}{
  \pause
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{3}{-.2}{2.5}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cgreen] plot[smooth,domain=0:3,samples=30] function{2-(x-1.5)**2};
      \tangent{1cm}{1cm}{2-pow(\x-1.5,2)}{0.75}
      \tangent{1cm}{1cm}{2-pow(\x-1.5,2)}{2.25}
    \end{scope}
  \end{tikzpicture}
  \pause\quad
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{3}{-.2}{2.5}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cgreen] plot[smooth,domain=0:3,samples=30] function{(x-1.5)**2};
      \tangent{1cm}{1cm}{pow(\x-1.5,2)}{0.75}
      \tangent{1cm}{1cm}{pow(\x-1.5,2)}{2.25}
    \end{scope}
  \end{tikzpicture}
  \pause\quad
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{3}{-.2}{2.5}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cgreen] plot[smooth,domain=0.4:2.7,samples=30] function{1+(x-1.5)**3};
      \tangent{1cm}{1cm}{1+pow(\x-1.5,3)}{0.75}
      \tangent{1cm}{1cm}{1+pow(\x-1.5,3)}{2.25}
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
\end{frame}