




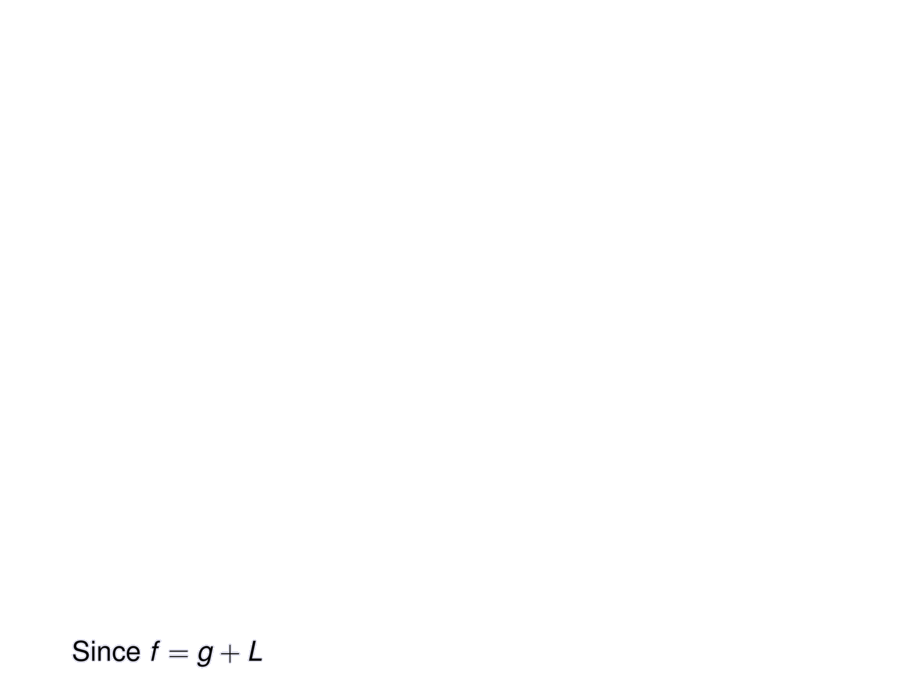

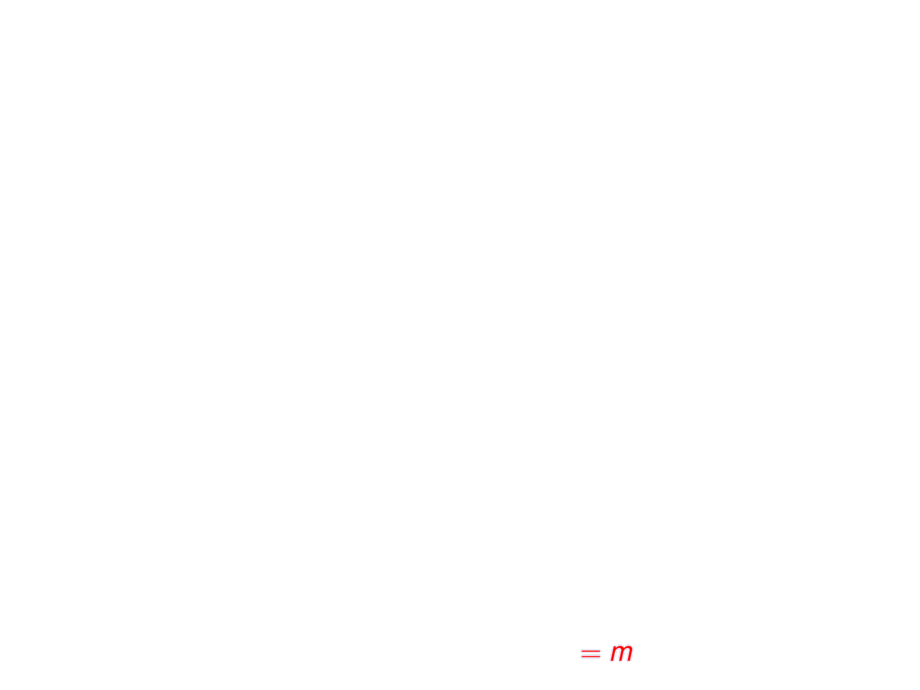


























































































34/66
\begin{frame}
\frametitle{Mean Value Theorem}
\begin{block}{Proof of the Mean Value Theorem}
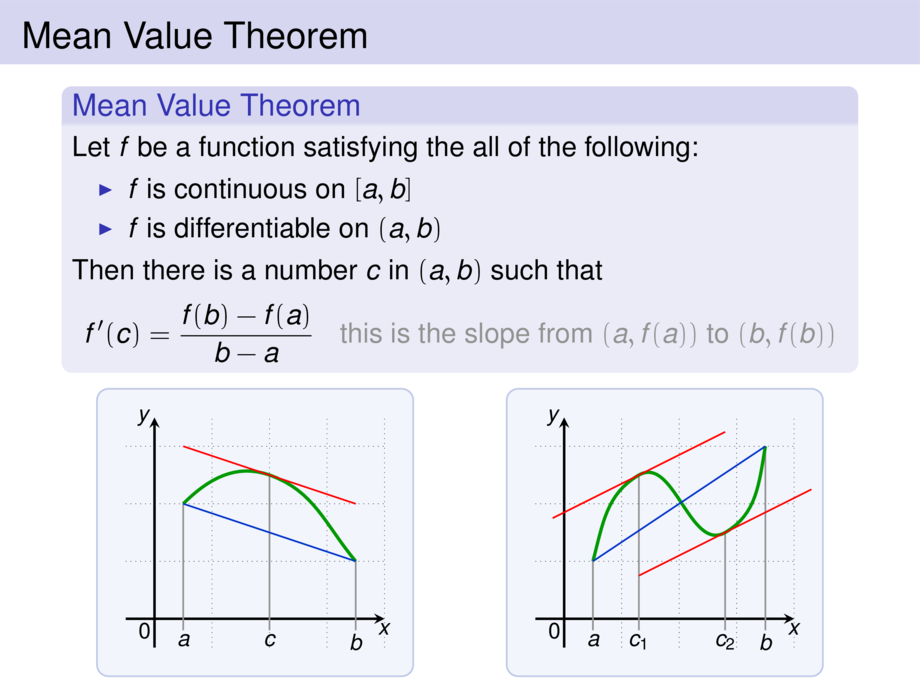
Let $f$ be a function satisfying the all of the following:
\begin{itemize}
\item $f$ is continuous on $[a,b]$
\item $f$ is differentiable on $(a,b)$
\end{itemize}
\pause
\begin{center}\vspace{-1ex}
\scalebox{.8}{
\begin{tikzpicture}[default,baseline=1cm]
\diagram{-.5}{4}{-.2}{2.5}{1}
\diagramannotatez
\draw[gray] (.5,2) -- node [black,at end,below] {$a$} (.5,-.2);
\draw[gray] (3.5,1) -- node [black,at end,below] {$b$} (3.5,-.2);
\mpause[4]{ \draw[gray] (2,2.5) -- node [black,at end,below] {$c$} (2,-.2); }
\begin{scope}[ultra thick]
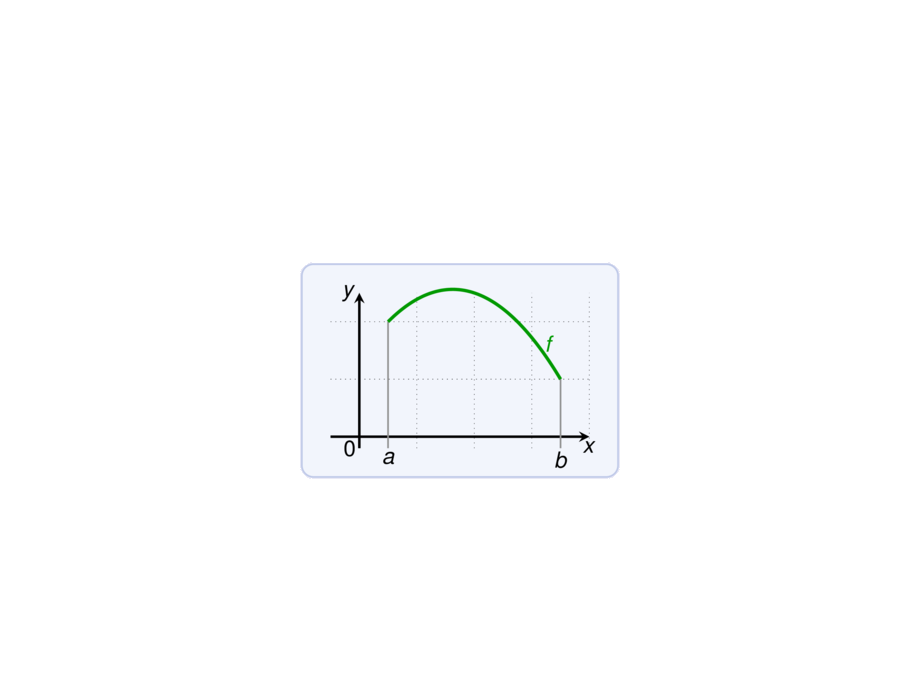
\draw[cgreen] plot[smooth,domain=.5:3.5,samples=30] function{3-((x-2)/1.5)**2 - (x-.5)/3} node[above,yshift=4mm,xshift=-2mm] {$f$};
\end{scope}
\mpause[1]{
\draw[cblue] (.5,2) -- node[below,pos=.8] {$L$} (3.5,1);
\node[include=cblue] at (.5,2) {};
\node[include=cblue] at (3.5,1) {};
}
\mpause[2]{
\begin{scope}[ultra thick]
\draw[cred] plot[smooth,domain=.5:3.5,samples=30] function{3-((x-2)/1.5)**2 - (x-.5)/3 - 2 + (x-.5)/3} node[above,yshift=4mm,xshift=-2mm] {$g$};
\end{scope}
}
% \node (a) at (2,2.5) {};
% \draw[cred] ($(a)+(-1.5,1.5/3)$) -- +(3,-3/3);
\end{tikzpicture}\vspace{-1ex}
}
\end{center}
\pause
Let \structure{$L = mx + n$} be the line through \structure{$(a,f(a))$} and \structure{$(b,f(b))$}.
\pause\smallskip
Define \alert{$g = f - L$}. \pause Then $g(a) = 0$ and $g(b) = 0$.
\pause\smallskip
By Rolle's Theorem there is $c$ in $(a,b)$ such that \alert{$g'(c) = 0$}.
\pause\smallskip
Since $f = g + L$ \pause we get \alert{$f'(c) = g'(c) + m \pause = m \pause = \frac{f(b)-f(a)}{b-a}$}.
\end{block}
\end{frame}

