\begin{frame}
  \frametitle{Mean Value Theorem}
  
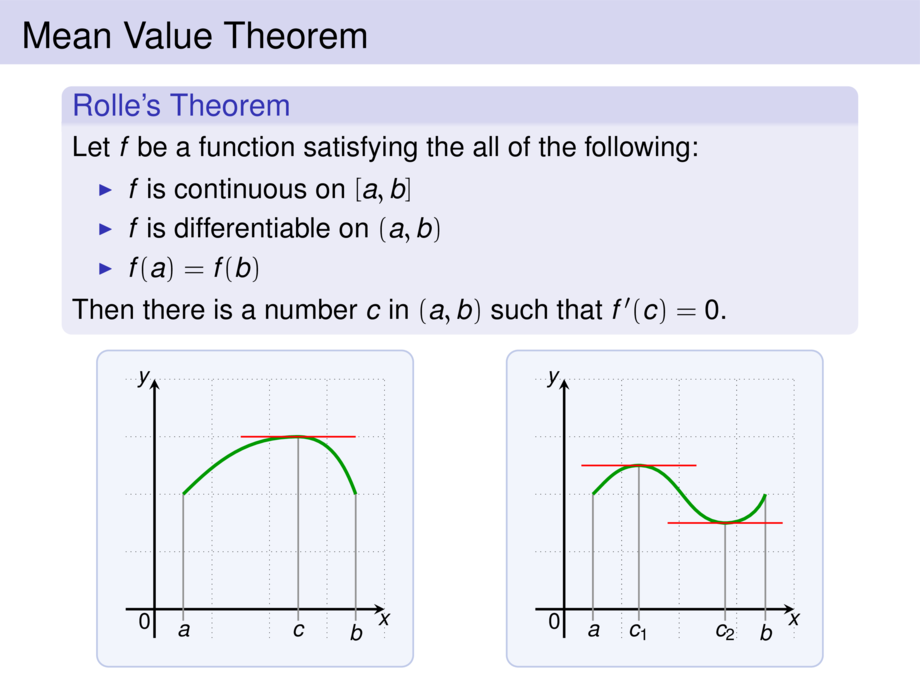
  \rolle
  \only<1>{
  \begin{center}
  \scalebox{.8}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{4}{-.5}{4}{1}
    \diagramannotatez
    \draw[gray] (.5,2) -- node [black,at end,below] {$a$} (.5,-.2);
    \draw[gray] (3.5,2) -- node [black,at end,below] {$b$} (3.5,-.2);
    \draw[gray] (2.5,3) -- node [black,at end,below] {$c$} (2.5,-.2);
    \begin{scope}[ultra thick]
      \draw[cgreen,ultra thick] (.5,2) to[out=45,in=180] (2.5,3) to[out=0,in=110] (3.5,2);
    \end{scope}
    \node (a) at (2.5,3) {};
    \draw[cred] ($(a)+(-1,0)$) -- +(2,0);
  \end{tikzpicture}
  }\hspace{1cm}
  \scalebox{.8}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{4}{-.5}{4}{1}
    \diagramannotatez
    \draw[gray] (.5,2) -- node [black,at end,below] {$a$} (.5,-.2);
    \draw[gray] (3.5,2) -- node [black,at end,below] {$b$} (3.5,-.2);
    \draw[gray] (1.3,2.5) -- node [black,at end,below] {$c_1$} (1.3,-.2);
    \draw[gray] (2.8,1.5) -- node [black,at end,below] {$c_2$} (2.8,-.2);
    \begin{scope}[ultra thick]
      \draw[cgreen,ultra thick] (.5,2) to[out=45,in=180] (1.3,2.5) to[out=0,in=180] (2.8,1.5) to[out=0,in=-110] (3.5,2);
    \end{scope}
    \node (a) at (1.3,2.5) {};
    \draw[cred] ($(a)+(-1,0)$) -- +(2,0);
    \node (a) at (2.8,1.5) {};
    \draw[cred] ($(a)+(-1,0)$) -- +(2,0);
  \end{tikzpicture}
  }
  \end{center}
  }
  \pause
  
  \begin{proof}
    \begin{itemize}
    \pause
      \item If $f$ is constant\pause, then $f'(c) = 0$ for all $c$ in $(a,b)$.
    \pause
      \item If $f$ is not constant\pause, then there is $x$ in $(a,b)$
        such that \vspace{-1ex}
        \begin{talign}
          f(x) > f(a) &&\text{ or }&& f(x) < f(a)
        \end{talign}
        \pause
        Assume $f(x) > f(a)$. \pause
        By the Extreme Value Theorem there is a $c$ in $[a,b]$ such that $f(c)$ is
        the absolute maximum. 
        \pause\medskip
        
        Then $c$ must be in $(a,b)$ and hence is a local maximum. \pause
        Hence $f'(c) = 0$ by Fermat's Theorem.\vspace{-3.8ex}
    \end{itemize}
  \end{proof}
  
  \vspace{10cm}
\end{frame}