\begin{frame}
  \frametitle{Exam Task from 2003}

  \vspace{-1ex}
  \begin{exampleblock}{}
    \begin{minipage}{.54\textwidth}
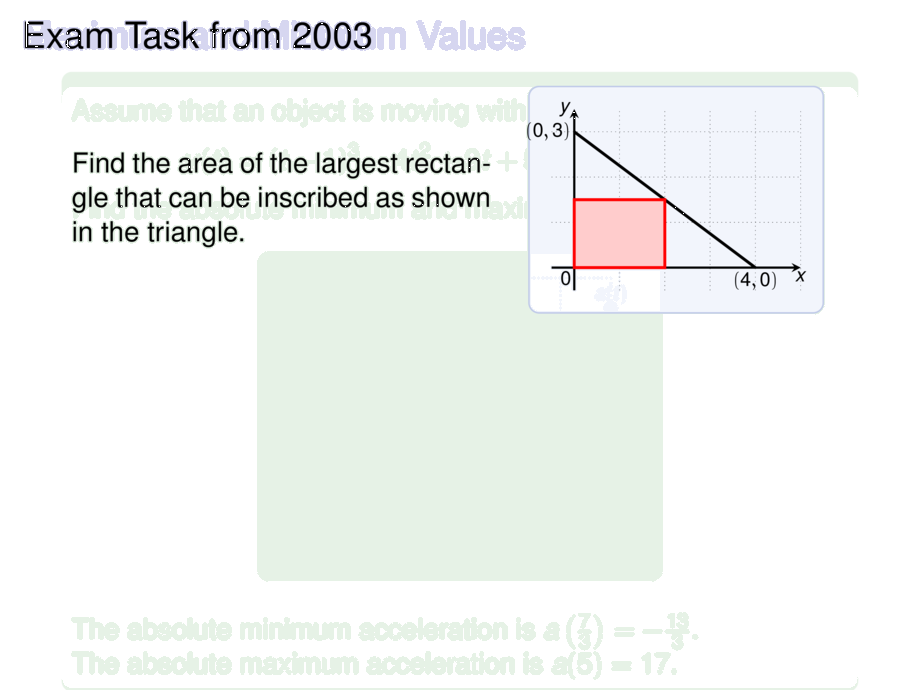
    Find the area of the largest rectangle that can be inscribed as shown
    in the triangle.
    \end{minipage}
    \begin{minipage}{.45\textwidth}
    \begin{center}
    \scalebox{.7}{
    \begin{tikzpicture}[default,baseline=1cm,scale=.9]
      \diagram{-.5}{5}{-.5}{3.5}{1}
      \diagramannotatez
      \begin{scope}[ultra thick]
        %\draw plot[smooth,domain=-.5:4,samples=30] function{ (x**3 - 3*x**2 + 1)/5};
        \draw[black] (0,3) -- node[at start,left] {$(0,3)$} node[at end,below] {$(4,0)$} (4,0);
        \draw[cred,fill=cred!20] (0,0) rectangle (2,1.5);
        \mpause[1]{ \node[below] at (2,0) {$x$}; }
      \end{scope}
    \end{tikzpicture}
    }
    \end{center}
    \end{minipage}  
    \pause\smallskip
    
    The line trough $(0,3)$ \& $(4,0)$ has the equation:
    \alert{$\ell(x) = \pause -\frac{3}{4}x + 3$}\hspace{-2ex}
    \pause\medskip
    
    The area $A$ of the rectangle depends on the width $x$:\vspace{-1ex}
    \begin{talign}
      A(x) &= \mpause[1]{x \cdot \ell(x)} \mpause[2]{ = x \cdot (-\frac{3}{4}x + 3)} 
         \mpause[3]{ = -\frac{3}{4}x^2 + 3x} 
        \quad \mpause[4]{\text{for $x$ in $[\mpause[5]{0},\mpause[5]{4}]$}}
      \\
        \mpause[6]{A'(x) }&\mpause[7]{= }\mpause[8]{-\frac{3}{2}x + 3}
      \quad\quad  \mpause[9]{A'(x) =0 \;\iff\;}\mpause[10]{\frac{3}{2}x = 3}\mpause[11]{\;\iff\; x = 2}
    \end{talign}
    \pause\pause\pause\pause\pause\pause\pause\pause\pause\pause\pause\pause
    Thus the only critical number is $2$. 
    The value of $A(x)$ at $0$, $2$, $4$:
    \begin{talign}
      A(0) = \mpause[1]{0}
      && \mpause[2]{A(2) =} \mpause[3]{3}
      && \mpause[4]{A(4) =} \mpause[5]{0}
    \end{talign}
    \pause\pause\pause\pause\pause\pause
    The the area of the largest rectangle is \alert{$3$}.
  \end{exampleblock}
\end{frame}