\begin{frame}
  \frametitle{Maximum and Minimum Values}
  
  \begin{exampleblock}{}
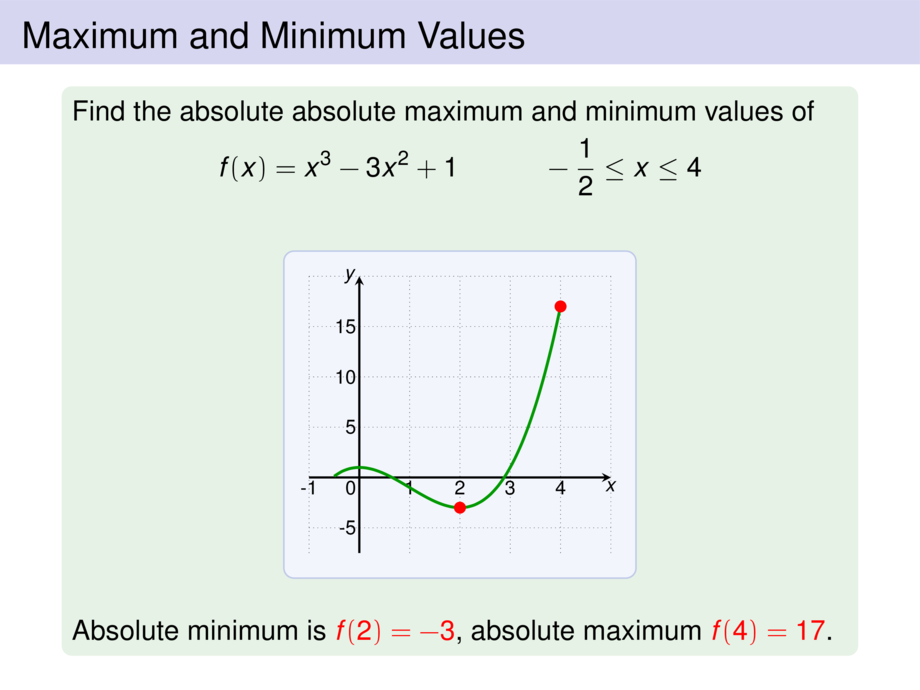
    Find the absolute absolute maximum and minimum values of 
    \begin{talign}
      f(x) = x^3 - 3x^2 + 1 \quad\quad\quad -\frac{1}{2} \le x \le 4
    \end{talign}%
    \only<-19>{%
    \pause
    Since $f$ is cont. on $[-\frac{1}{2},4]$ we can use Closed Interval Method.
    \begin{talign}
      f'(x) = \mpause[1]{3x^2 - 6x}\mpause[2]{ = 3x(x - 2)}
    \end{talign}
    \pause\pause\pause
    We have $f'(x) = 0$ if \pause \quad \alert{$x = 0$} \quad or \quad \alert{$x = 2$}. \quad\pause
    \alert{Both in $[-\frac{1}{2},4]$!}\\\pause
    No other critical values since $f'(x)$ exists for all $x$.
    \pause\medskip
    
    The values of $f$ at the critical numbers are:
    \begin{talign}
      f(0) = \mpause[1]{1} &&
      \mpause[2]{f(2) =}\mpause[2]{ -3}
    \end{talign}
    \pause\pause\pause
    The values of $f$ at the end points of the interval are:
    \begin{talign}
      f(-\frac{1}{2}) = \mpause[1]{-\frac{1}{8} - 3\frac{1}{4} + 1} 
%       \mpause[2]{= -\frac{7}{8} + 1} 
      \mpause[2]{= \frac{1}{8}} &&&&
      \mpause[3]{f(4) =} \mpause[4]{4\cdot 16 - 3\cdot 16 + 1} \mpause[5]{= 17}
    \end{talign}
    \pause\pause\pause\pause\pause\pause
    }
    \only<20>{
    \begin{center}
    \scalebox{.7}{
    \begin{tikzpicture}[default,baseline=1cm]
      \diagram{-1}{5}{-1.5}{4}{1}
      \diagramannotateyy{-1/-5,1/5,2/10,3/15}
      \diagramannotatex{-1,1,2,3,4}
      \diagramannotatez
      \begin{scope}[cgreen,ultra thick]
        \draw plot[smooth,domain=-.5:4,samples=30] function{ (x**3 - 3*x**2 + 1)/5};
        \node[include=cred] at (2,-3/5) {};
        \node[include=cred] at (4,17/5) {};
      \end{scope}
    \end{tikzpicture}
    }
    \end{center}
    \medskip
    }%
    Absolute minimum is \alert{$f(2) = -3$}, \pause absolute maximum \alert{$f(4) = 17$}.
  \end{exampleblock}
  \vspace{10cm}
\end{frame}