\begin{frame}
  \frametitle{Maximum and Minimum Values}

  \begin{block}{Fermat's Theorem}
    \alert{If} $f$ has a local maximum or minimum at $c$ and $f'(c)$ exists, \\
    \alert{then} $f'(c) = 0$.
  \end{block}
  \pause\medskip

  \begin{alertblock}{}
    The reverse statement is not true!
    Having $f'(c) = 0$ does not guarantee that $f(c)$ is a minimum or maximum.
  \end{alertblock}
  \pause\bigskip
  
  \begin{minipage}{.4\textwidth}
  \begin{center}
  \scalebox{.7}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-2}{2}{-2.5}{2.5}{1}
    \diagramannotatey{-1,1,2}
    \diagramannotatex{-1,1}
    \diagramannotatez
    \begin{scope}[cgreen,ultra thick]
      \draw plot[smooth,domain=-1.4:1.4,samples=30] function{x**3};
    \end{scope}
    \begin{scope}[very thick]
    \node[cgreen,include] (a) at (0,0) {};
    \draw[cred] ($(a)+(-1cm,0)$) -- ($(a)+(1cm,0)$);
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
  \end{minipage}
  \begin{minipage}{.59\textwidth}
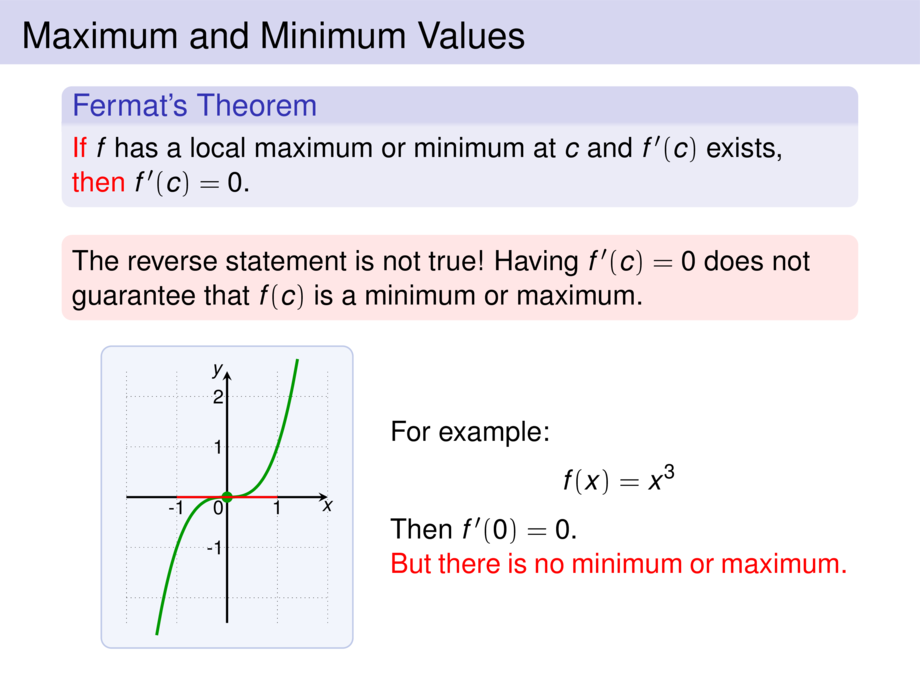
    For example:
    \begin{talign}
      f(x) = x^3
    \end{talign}
    \pause
    Then $f'(0) = 0$.\\
    \pause
    \alert{But there is no minimum or maximum.} 
  \end{minipage}
  \vspace{10cm}
\end{frame}