\begin{frame}
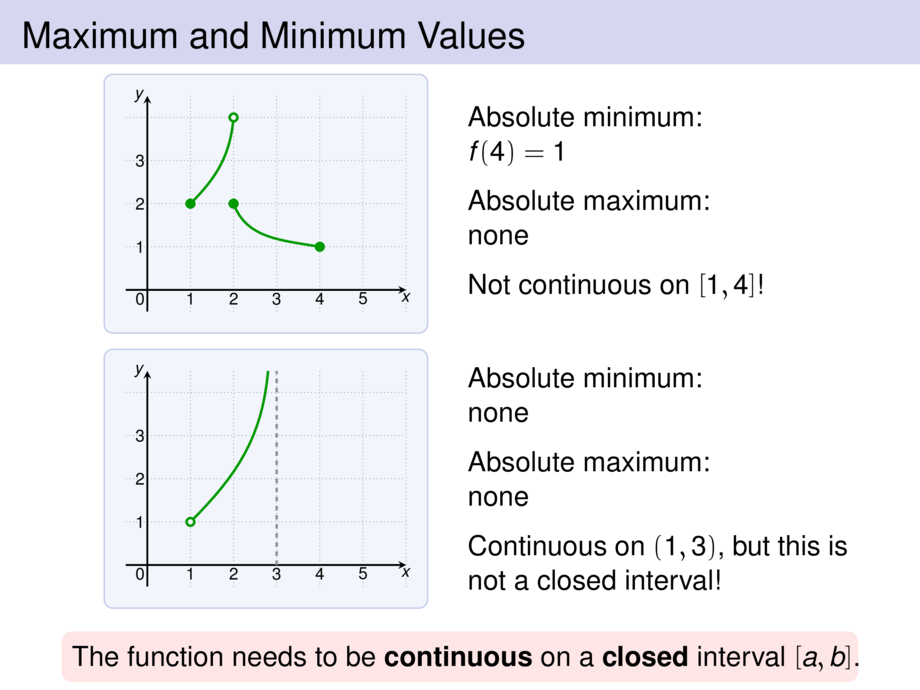
  \frametitle{Maximum and Minimum Values}
  
  \begin{minipage}{.5\textwidth}
  \begin{center}
  \scalebox{.6}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{6}{-.5}{4.5}{1}
    \diagramannotatey{1,2,3}
    \diagramannotatex{1,2,3,4,5}
    \diagramannotatez
    \begin{scope}[cgreen,ultra thick]
      %\draw plot[smooth,domain=-1:4,samples=200] function{(3*x**4 - 16*x**3 + 18*x**2)/15};
      \draw (1,2) to[out=45,in=-95] (2,4);
      \draw (2,2) to[out=-70,in=170] (4,1); 
      \node[include] at (1,2) {};
      \node[exclude] at (2,4) {};
      \node[include] at (2,2) {};
      \node[include] at (4,1) {};
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
  \end{minipage}~%
  \begin{minipage}{.49\textwidth}
    \pause
    Absolute minimum:\\\pause
    $f(4) = 1$
    \pause\medskip
    
    Absolute maximum:\\\pause
    none
    \pause\medskip
    
    Not continuous on $[1,4]$!
  \end{minipage}
  \pause\medskip
  
  \begin{minipage}{.5\textwidth}
  \begin{center}
  \scalebox{.6}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{6}{-.5}{4.5}{1}
    \diagramannotatey{1,2,3}
    \diagramannotatex{1,2,3,4,5}
    \diagramannotatez
    \begin{scope}[cgreen,ultra thick]
      %\draw plot[smooth,domain=-1:4,samples=200] function{(3*x**4 - 16*x**3 + 18*x**2)/15};
      \draw (1,1) to[out=45,in=-95] (2.8,4.5);
      \node[exclude] at (1,1) {};
      \draw[gray,dashed] (3,0) -- (3,4.5);
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
  \end{minipage}~%
  \begin{minipage}{.49\textwidth}
    \pause
    Absolute minimum:\\\pause
    none
    \pause\medskip
    
    Absolute maximum:\\\pause
    none
    \pause\medskip
    
    Continuous on $(1,3)$,
    but this is not a closed interval!
  \end{minipage}
  \pause\smallskip
  
  \begin{alertblock}{}
  The function needs to be \emph{continuous} on a \emph{closed} interval $[a,b]$.\hspace{-10ex}
  \end{alertblock}
  \vspace{10cm}
\end{frame}