\begin{frame}
  \frametitle{Maximum and Minimum Values}

    \begin{center}\vspace{-2ex}
    \scalebox{.85}{
    \begin{tikzpicture}[default,baseline=1cm]
      \def\diay{}
      \diagram{-1}{5}{-.5}{3.5}{1}
      \diagramannotatez
      \def\xa{.5}
      \def\xb{1.5}
      \def\xc{2.5}
      \def\xd{3}
      \def\xe{4}
      \def\xf{4.5}
      \begin{scope}[gray]
        \draw (\xa,1) -- node[black,at end,below] {$a$} (\xa,-.2);
        \draw (\xb,2.5) -- node[black,at end,below] {$b$} (\xb,-.2);
        \draw (\xc,2.8) -- node[black,at end,below] {$c$} (\xc,-.2);
        \draw (\xd,1.5) -- node[black,at end,below] {$d$} (\xd,-.2);
        \draw (\xe,3.5) -- node[black,at end,below] {$e$} (\xe,-.2);
        \draw (\xf,1.5) -- node[black,at end,below] {$f$} (\xf,-.2);
      \end{scope}
      \begin{scope}[cgreen,ultra thick]
         \draw (\xa,1) to[out=80,in=220] node[include,at start] {} node[include,at end] {} (\xb,2.5); 
         \draw (\xb,1.5) to[out=80,in=200] node[exclude,at start] {} node[exclude,at end] {} (\xc,2.8); 
         \draw (\xc,2) to[out=-70,in=180] node[include,at start] {} (\xd,1.5)  to[out=0,in=-90,looseness=.5] (\xe,3.5) to[out=-90,in=120,looseness=.5] node[include,at end] {} (\xf,1.5);
      \end{scope}
    \end{tikzpicture}
    }
    \end{center}
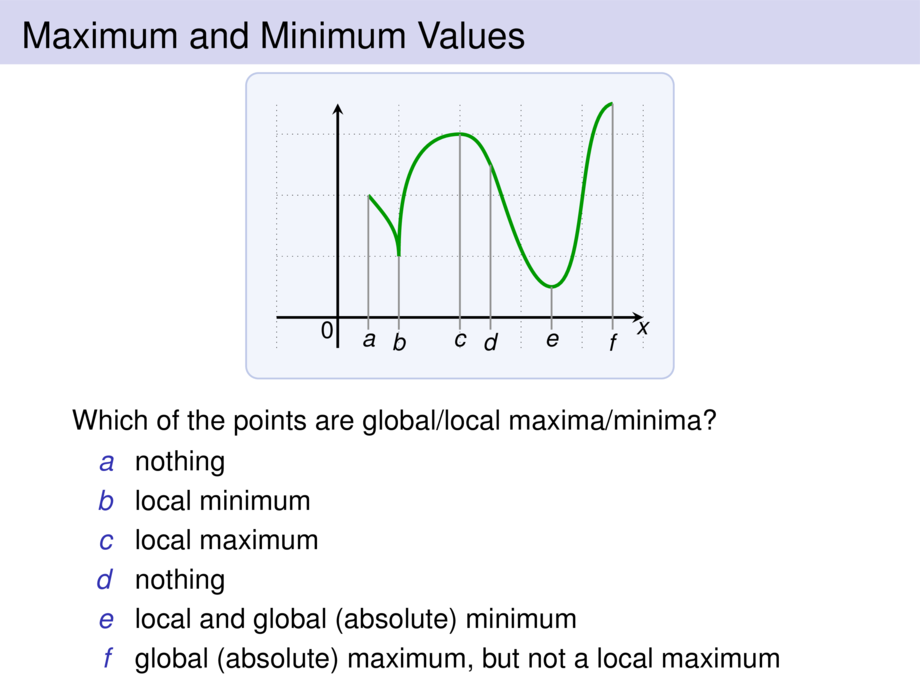
    Which of the points are global/local maxima/minima?
    \begin{itemize}
    \pause
      \item [$a$] \ \pause global (absolute) minimum, but not a local minimum
    \pause
      \item [$b$] \ \pause local maximum
    \pause
      \item [$c$] \ \pause nothing
    \pause
      \item [$d$] \ \pause local minimum
    \pause
      \item [$e$] \ \pause local and global (absolute) maximum
    \pause
      \item [$f$] \ \pause nothing
    \end{itemize}
\end{frame}