\begin{frame}
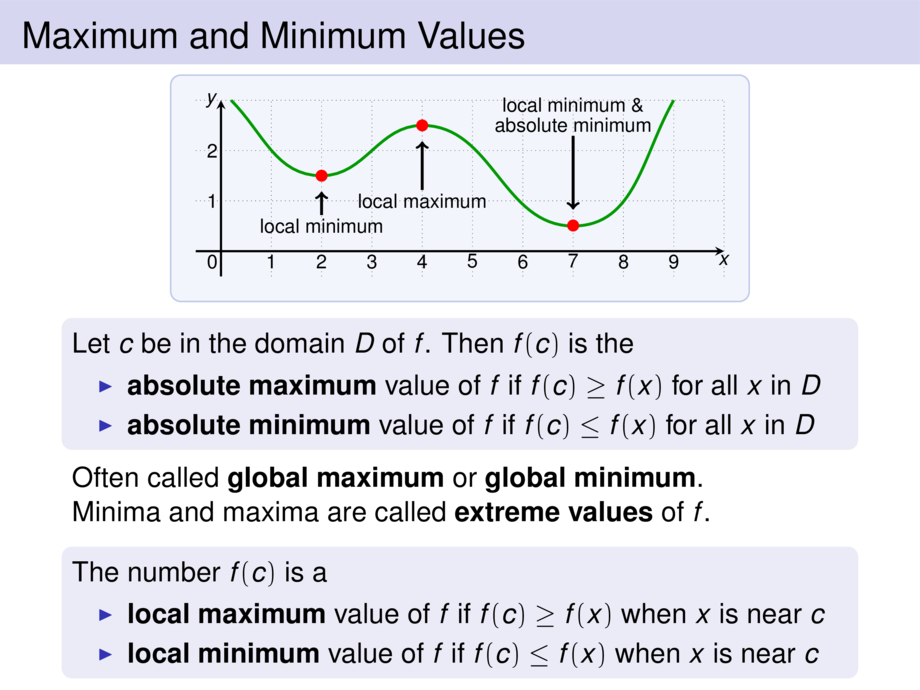
  \frametitle{Maximum and Minimum Values}
  
  \begin{exampleblock}{}
    Where does
    \begin{talign}
      f(x) = x^2
    \end{talign}
    have local / global minima or maxima?
    \pause\bigskip
    
    The value \alert{$f(0) = 0$} is absolute and local minimum since:
    \begin{talign}
      f(0) = 0 \le x^2 = f(x) \quad\text{for all $x$}
    \end{talign}  
    \pause
    The function has no local or global maxima.
  \end{exampleblock}
  \pause
  
  \begin{exampleblock}{}
    \begin{minipage}{.7\textwidth}
    Where does
    \begin{talign}
      f(x) = x^3
    \end{talign}
    have (local or global) minima or maxima?
    \pause\bigskip
    
    The function has no local or global extrema.
    \end{minipage}
    \pause
    \begin{minipage}{.29\textwidth}
    \scalebox{.6}{
    \begin{tikzpicture}[default,baseline=1cm]
      \diagram{-2}{2}{-2}{2.5}{1}
      \diagramannotatey{1,2}
      \diagramannotatex{1,2}
      \diagramannotatez
      \begin{scope}[ultra thick]
        \draw[cgreen,ultra thick] plot[smooth,domain=-1.25:1.35,samples=200] function{x**3};
      \end{scope}
    \end{tikzpicture}
    }
    \end{minipage}
  \end{exampleblock}
\end{frame}