
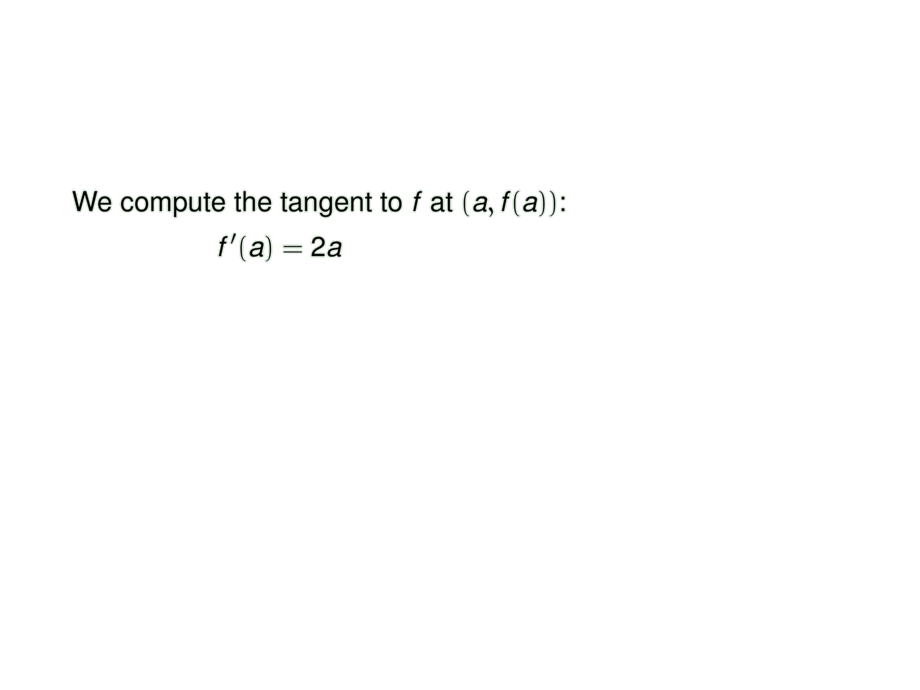
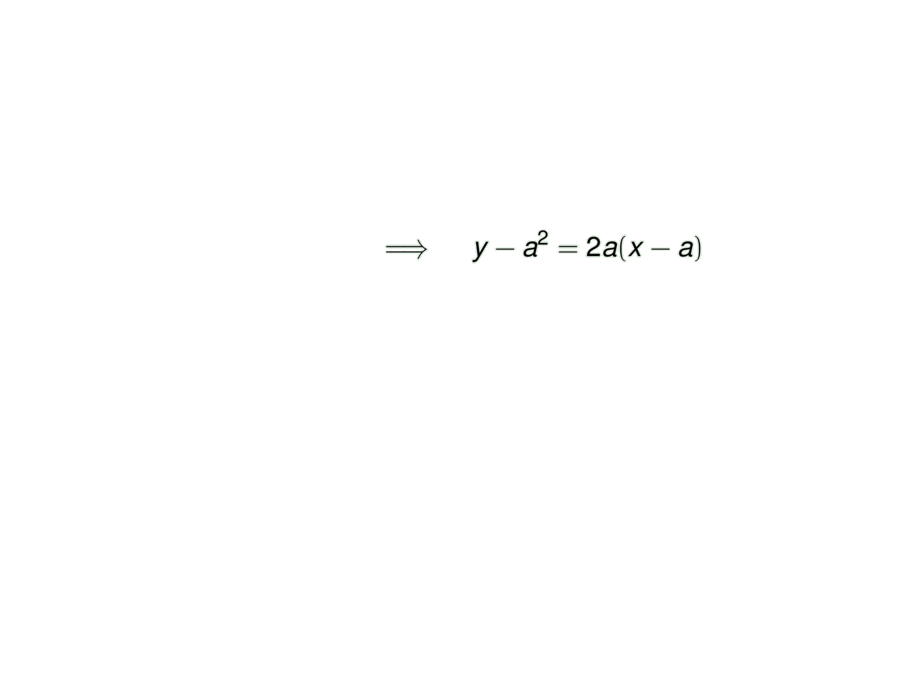
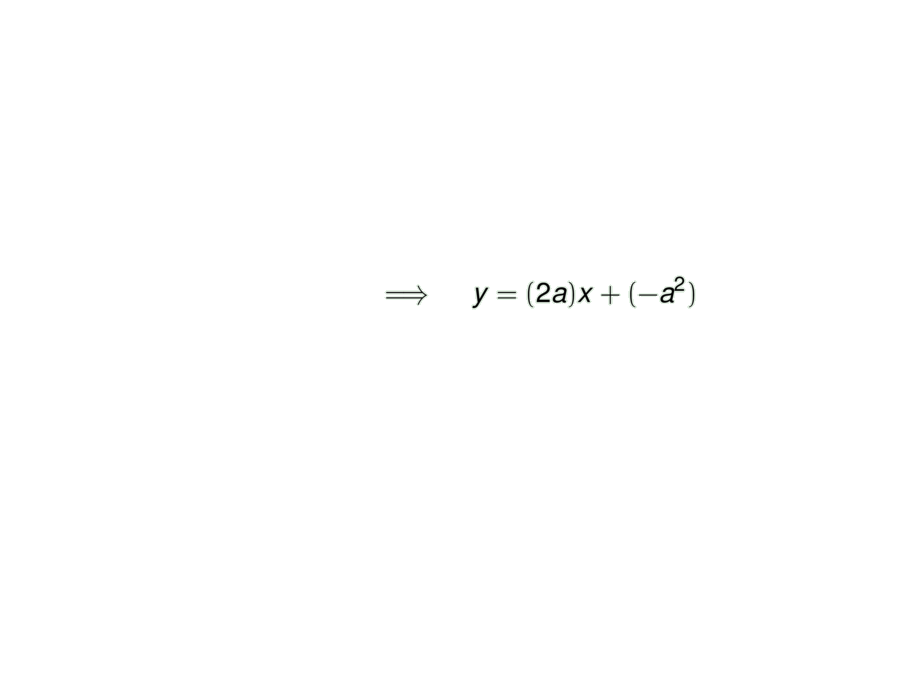

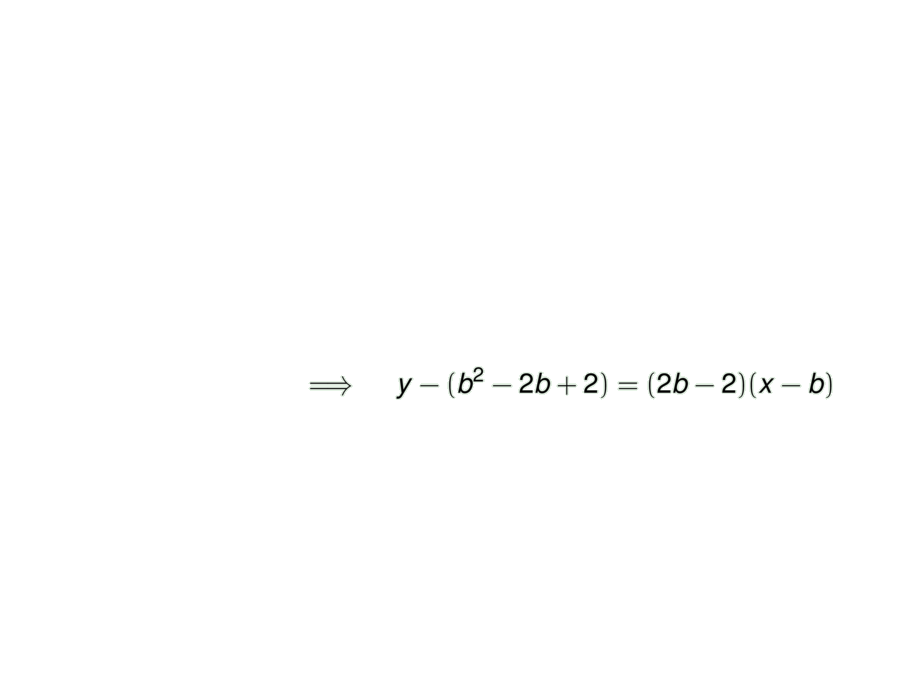



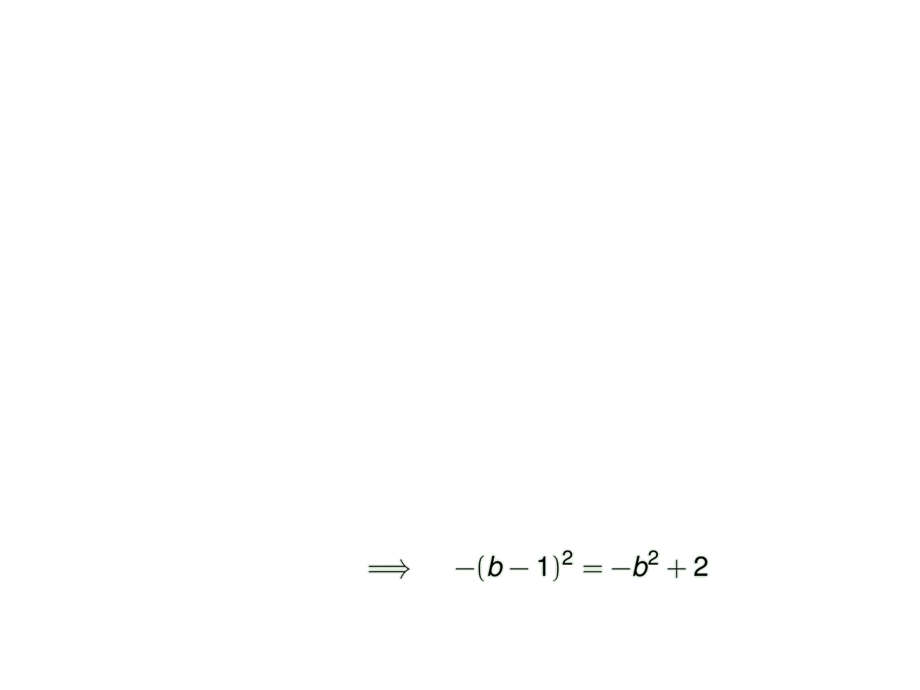
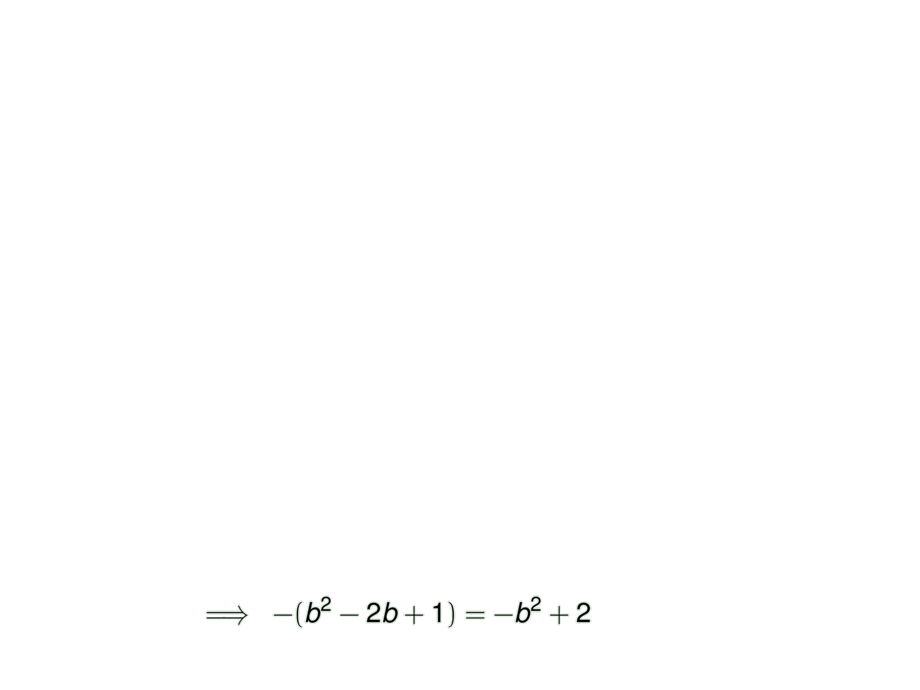
























































































138/177
\begin{frame}
\frametitle{2nd Midterm Exam - Review}
\begin{exampleblock}{}
Is there a line that is tangent to both curves $f$ and $g$?\vspace{-1.2ex}
\begin{align*}
f(x) = x^2 && g(x) = x^2 - 2x + 2
\end{align*}\vspace{-3.5ex}
\pause
We compute the tangent to $f$ at $(a,f(a))$:\vspace{-1.2ex}
\begin{align*}
f'(a) = 2a &\mpause[1]{\quad\implies\quad y-a^2 = 2a(x-a)}\\
&\mpause[2]{\quad\implies\quad y = (2a)x + (- a^2)}
\end{align*}\vspace{-3.5ex}
\pause\pause\pause
We compute the tangent to $g$ at $(b,g(b))$:\vspace{-1.2ex}
\begin{align*}
g'(b) = 2b-2 &\mpause[1]{\quad\implies\quad y-(b^2-2b+2) = (2b-2)(x-b)} \\
&\mpause[2]{\quad\implies\quad y = (2b - 2)x + (- b^2 + 2)}
\end{align*}\vspace{-3.5ex}
\pause\pause\pause
The tangents are equal if:\vspace{-1.2ex}
\begin{align*}
2a &= 2b - 2 \mpause[1]{\quad\implies\quad a = b-1 \mpause[5]{\;\implies\; \alert{a = 1/2}}}\\
-a^2 &= -b^2 + 2 \mpause[2]{\quad\implies\quad -(b-1)^2 = -b^2 + 2}\\
&\mpause[3]{\implies\; -(b^2-2b+1) = -b^2 + 2}
\mpause[4]{\;\implies\; \alert{b = 3/2}}
\end{align*}\vspace{-3.5ex}
\pause\pause\pause\pause\pause\pause
Thus the line $y = x - 1/4$ is tangent to both curves.
\end{exampleblock}
\end{frame}

