


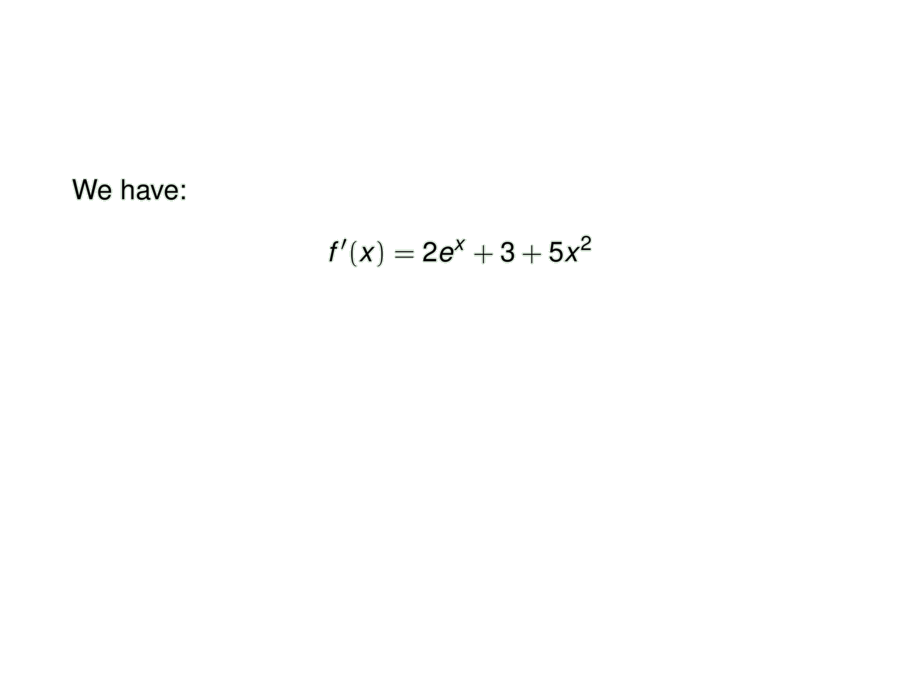
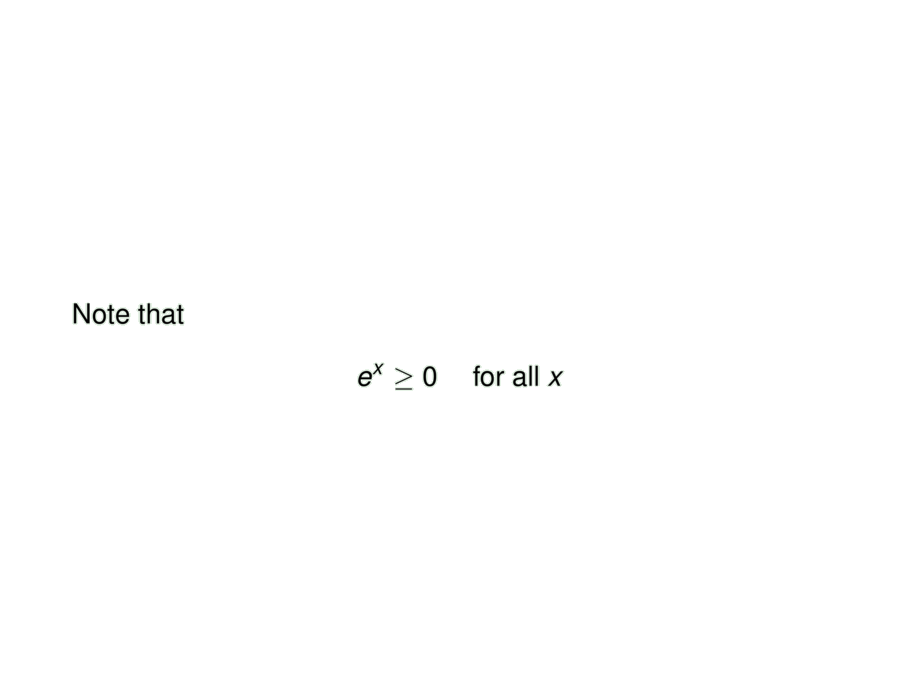

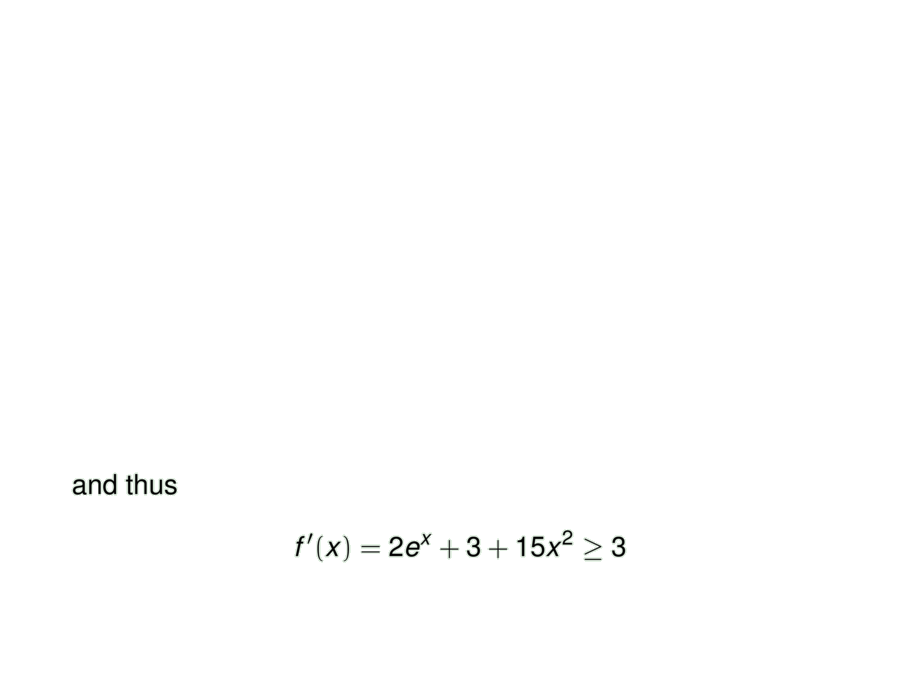





























































































88/177
\begin{frame}
\frametitle{2nd Midterm Exam - Review}
\begin{exampleblock}{}
Show that $f(x) = 2e^x + 3x + 15x^3$
has no tangent with slope $2$.
\pause\bigskip
We have:
\begin{align*}
f'(x) = 2e^x + 3 + 5x^2
\end{align*}
\pause
Note that
\begin{align*}
e^x \ge 0 &\quad\text{ for all $x$}\\
\mpause[1]{x^2 \ge 0} &\mpause[1]{\quad\text{ for all $x$}}
\end{align*}
\pause\pause
and thus
\begin{align*}
f'(x) = 2e^x + 3 + 15x^2 \ge 3
\end{align*}
\pause
The slope of the curve $f(x)$ is $\ge 3$ everywhere.\\\pause
Hence the curve cannot have a tangent with slope $2$.
\end{exampleblock}
\end{frame}

