



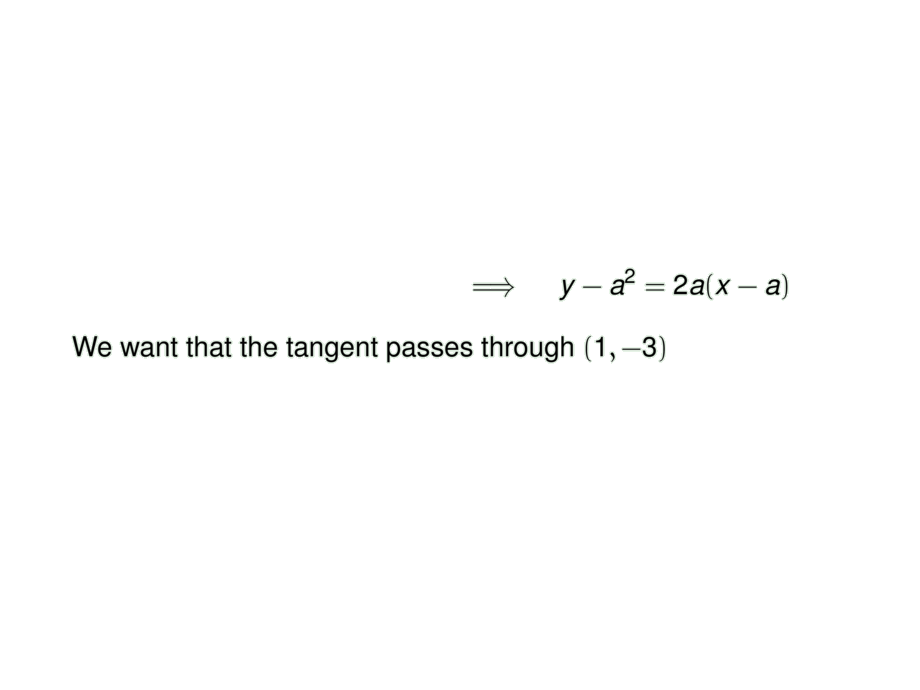
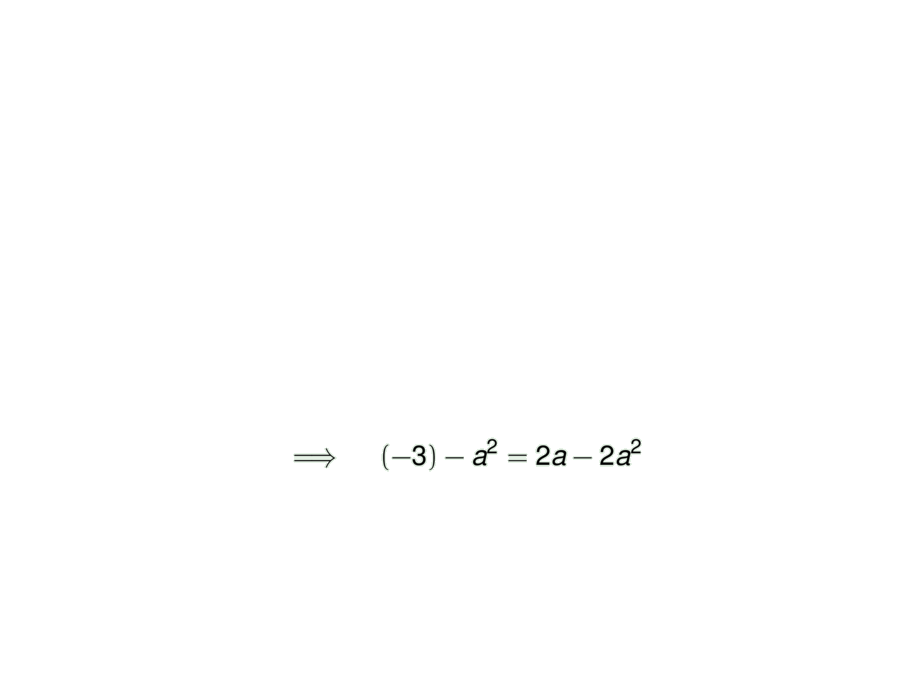





























































































80/177
\begin{frame}
\frametitle{2nd Midterm Exam - Review}
\begin{exampleblock}{}
Let $f(x) = x^2$.
Find $a > 0$ such that the tangent to the curve at the point $(a,f(a))$ passes through the point $(1,-3)$.
\pause\bigskip
We have $f'(x) = 2x$. \pause Thus the tangent through $(a,f(a))$ is
\begin{align*}
y - f(a) = f'(a)\cdot (x - a)
\mpause[1]{\quad\implies\quad y - a^2 = 2a(x - a)}
\end{align*}
\pause
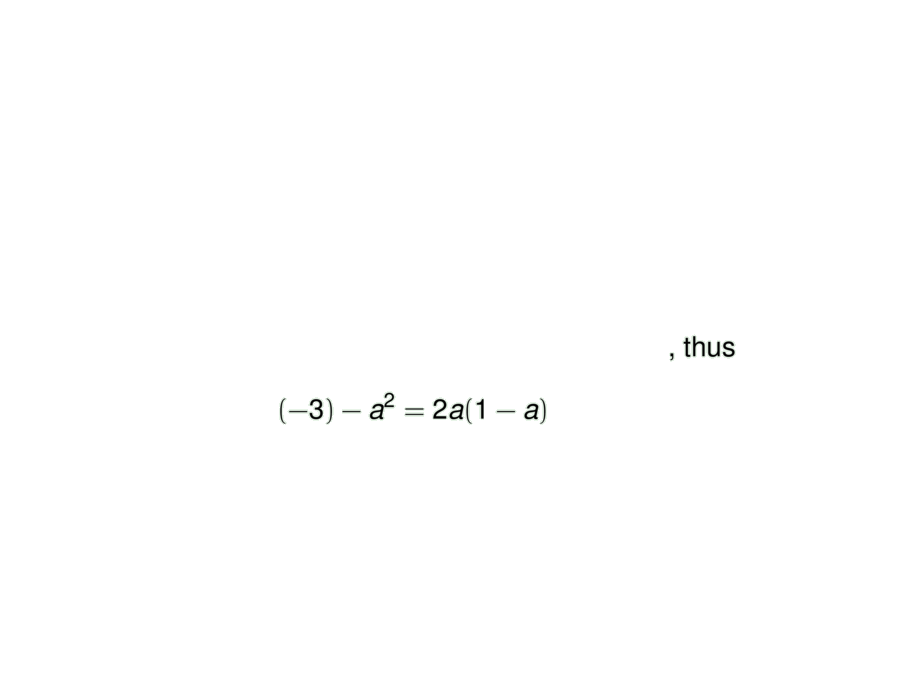
We want that the tangent passes through $(1,-3)$\pause, thus
\begin{align*}
&(-3) - a^2 = 2a(1 - a)\\
&\mpause[1]{\implies\quad (-3) - a^2 = 2a - 2a^2}\\
&\mpause[2]{\implies\quad a^2 - 2a -3 = 0}\\
&\mpause[3]{\implies\quad a = 1 \pm \sqrt{1 + 3}}
\end{align*}
\pause\pause\pause\pause
Thus $a = 3$ \quad\textcolor{gray}{(recall that we were searching for $a > 0$)}\\\pause
The tangent is \quad $y - 9 = 6(x - 3)$
\end{exampleblock}
\end{frame}

