


































































































67/87
\begin{frame}
\frametitle{Related (Dependent) Rates}
\begin{exampleblock}{}
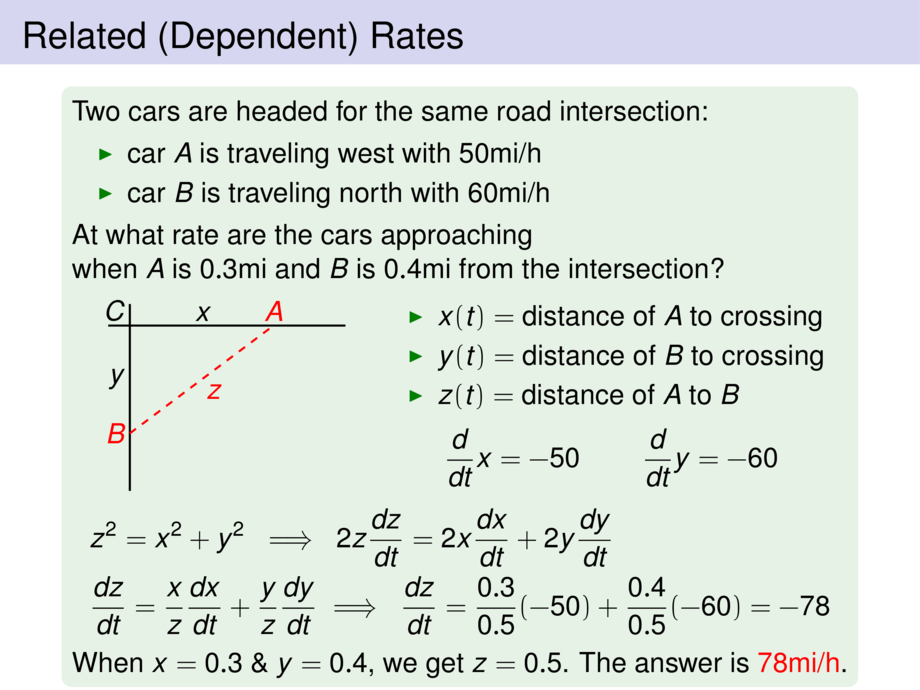
Two cars are headed for the same road intersection:
\begin{itemize}
\item car $A$ is traveling west with $50$mi/h
\item car $B$ is traveling north with $60$mi/h
\end{itemize}
At what rate are the cars approaching \\
when $A$ is $0.3$mi and $B$ is $0.4$mi
from the intersection?
\medskip
\begin{minipage}{.39\textwidth}
\begin{center}
\begin{tikzpicture}[default]
\draw (-0.3,0) -- node[pos=.4,above] {$\mpause[1]{x}$} (3,0);
\draw (0,.3) -- node[pos=.4,left] {$\mpause[2]{y}$} (0,-2.3);
\node at(0,0) [anchor=south east] {$C$};
\begin{scope}[cred]
\draw[dashed] (0,-1.5) -- node[below,anchor=north west] {$\mpause[3]{z}$} node [at start,left] {$B$} node [at end,above] {$A$} (2,0);
\end{scope}
% \begin{scope}
% \mpause[4]{
% \draw[->] (2.3,.5) -- node [above] {$\frac{d}{dt}x = -50$} ++(-.6,0);
% }
% \mpause[5]{
% \draw[->] (-.5,-1.8) -- node [left] {$\frac{d}{dt}y = -60$} ++(0,.6);
% }
% \end{scope}
\end{tikzpicture}
\end{center}
\end{minipage}
\begin{minipage}{.59\textwidth}
\begin{itemize}
\pause
\item $x(t) =$ distance of $A$ to crossing
\pause
\item $y(t) =$ distance of $B$ to crossing
\pause
\item $z(t) =$ distance of $A$ to $B$
\end{itemize}
\pause
\begin{malign}
\frac{d}{dt}x = -50 && \frac{d}{dt}y = -60
\end{malign}
\end{minipage}
\pause
\begin{talign}
&z^2 = x^2 + y^2
% \mpause[1]{\;\implies\; \frac{d}{dt}z^2 = \frac{d}{dt} (x^2 + y^2)}\\
\mpause[1]{\;\implies\; 2z\frac{dz}{dt} = 2x\frac{dx}{dt} + 2y\frac{dy}{dt}}\\
&\mpause[2]{\frac{dz}{dt} = \frac{x}{z}\frac{dx}{dt} + \frac{y}{z}\frac{dy}{dt}}
\mpause[5]{\implies\; \frac{dz}{dt} = \frac{0.3}{0.5}(-50) + \frac{0.4}{0.5}(-60)}
\mpause[6]{=-78}
\end{talign}
\pause\pause\pause
When $x = 0.3$ \& $y = 0.4$, we get $z = \pause 0.5$.
\pause\pause\pause
The answer is \alert{$78$mi/h}.
\end{exampleblock}
\end{frame}

