


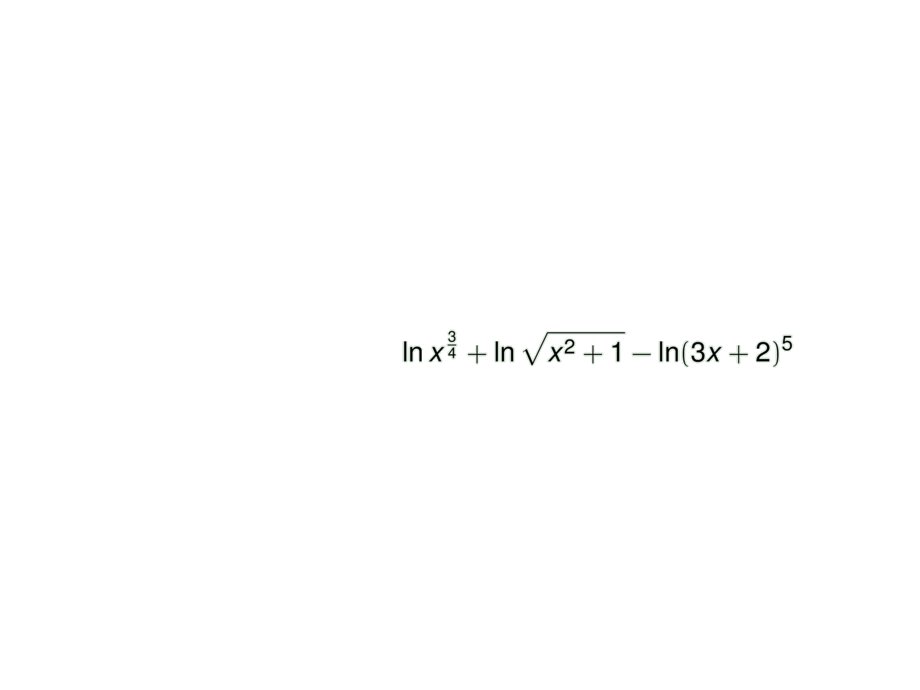
































































































42/78
\begin{frame}
\frametitle{Logarithmic Differentiation}
The following method is called \emph{logarithmic differentiation}.
\begin{exampleblock}{}
Differentiate
\begin{talign}
y = \frac{ x^{\frac{3}{4}}\cdot \sqrt{x^2+1} }{ (3x+2)^5 }
\end{talign}
\pause
\only<-6>{%
We take logarithms on both sides:
\begin{talign}
\ln y = \ln \frac{ x^{\frac{3}{4}}\cdot \sqrt{x^2+1} }{ (3x+2)^5 }
&= \mpause[1]{\ln x^{\frac{3}{4}} + \ln \sqrt{x^2+1} - \ln(3x+2)^5 }\\
&\mpause[2]{= \frac{3}{4} \ln x + \frac{1}{2}\ln(x^2+1) - 5\ln(3x+2) }
\end{talign}
\pause\pause\pause
We use implicit differentiation:
\begin{talign}
\frac{d}{dx} \ln y &= \frac{3}{4} \frac{d}{dx}\ln x + \frac{1}{2} \frac{d}{dx}\ln(x^2+1) - 5 \frac{d}{dx}\ln(3x+2) \\[1ex]
\mpause[1]{\frac{1}{y}y'} &\mpause[1]{= \frac{3}{4} \cdot \frac{1}{x} + \frac{1}{2} \cdot \frac{1}{x^2+1}\cdot 2x - 5\frac{1}{3x+2}\cdot 3 }
\end{talign}
}%
\only<7->{
\pause[7]%
We have:
\begin{talign}
\frac{1}{y}y' &= \frac{3}{4} \cdot \frac{1}{x} + \frac{1}{2} \cdot \frac{1}{x^2+1}\cdot 2x - 5\frac{1}{3x+2}\cdot 3
\end{talign}
\pause
Solving for $y'$ yields:
\begin{talign}
y' = y\left(\frac{3}{4x} + \frac{x}{x^2+1} - \frac{15}{3x+2}\right)
\end{talign}
\pause
Hence
\begin{talign}
y' = \frac{ x^{\frac{3}{4}}\cdot \sqrt{x^2+1} }{ (3x+2)^5 } \cdot \left(\frac{3}{4x} + \frac{x}{x^2+1} - \frac{15}{3x+2}\right)
\end{talign}
}
\end{exampleblock}
\vspace{10cm}
\end{frame}

