\begin{frame}
  \frametitle{Implicit Differentiation}

  \begin{block}{}
  We can use \emph{implicit differentiation}:
  \begin{itemize}
  \pause
    \item differentiate both sides of the equation w.r.t. $x$, and
  \pause
    \item then solve for $y'$, that is, for $\frac{dy}{dx}$
  \end{itemize}
  \end{block}
  \pause
  
  \begin{exampleblock}{}
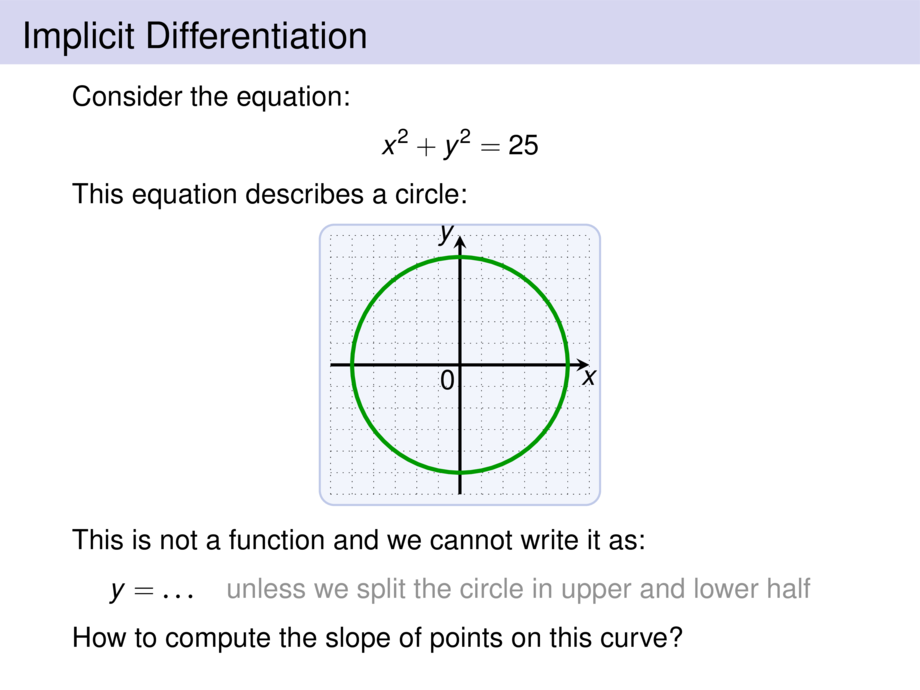
  We differentiate $x^2 + y^2 = 25$ implicitly.
  \pause
  We have
  \begin{talign}
    &\frac{d}{dx}(x^2 + y^2) = \frac{d}{dx} 25 \\[.5ex]
    &\mpause[1]{ \frac{d}{dx} x^2 + \frac{d}{dx} y^2 = 0 } \\[.5ex]
    &\mpause[2]{ 2x + \frac{d}{dx} y^2 = 0 } \hspace{1cm} \mpause[3]{ \text{\textcolor{gray}{$y$ is a function of $x$ $\implies$ chain rule}} }\\[.5ex]
    &\mpause[4]{ 2x + \frac{d}{dy}(y^2) \frac{d}{dx}y = 0 } \\[.5ex]
    &\mpause[5]{ 2x + 2y \frac{d}{dx}y = 0 } 
    \mpause[6]{\;\;\implies\;\; \frac{d}{dx}y = -\frac{x}{y} } 
    \mpause[7]{\;\;\implies\;\; \frac{dy}{dx} = -\frac{x}{y} } 
  \end{talign}
  \end{exampleblock}
  \vspace{10cm}
\end{frame}