


































































































21/93
\begin{frame}
\frametitle{Derivatives of Trigonometric Functions}
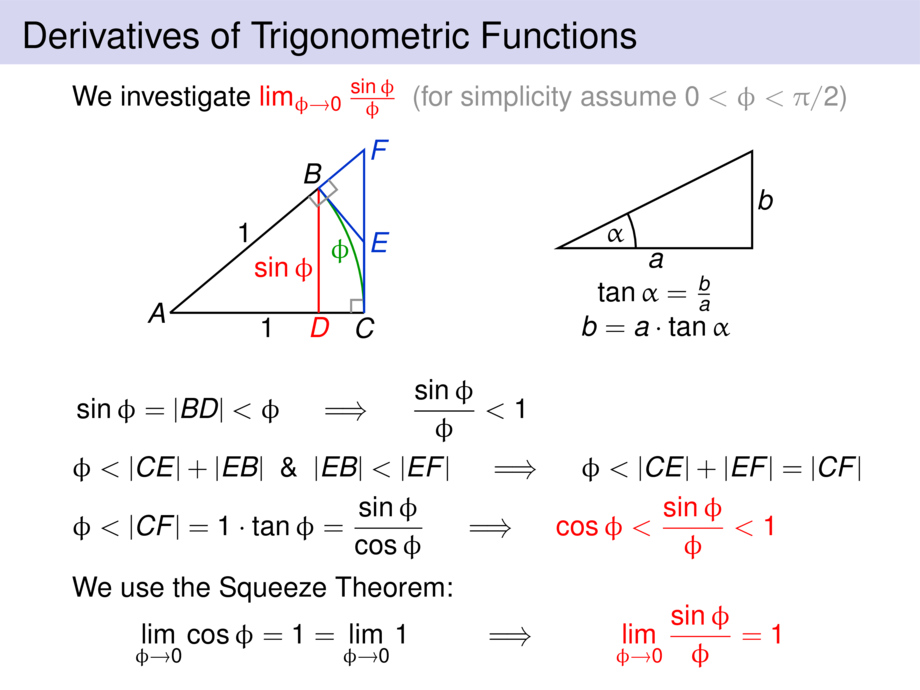
We investigate \alert{$\lim_{\phi\to 0}\frac{\sin \phi}{\phi}$}
\pause\hfill \textcolor{gray}{(for simplicity assume $0 < \phi < \pi/2$)}
\pause
\begin{center}
\begin{tikzpicture}[default,scale=.9]
\coordinate (a) at (0,0);
\coordinate (b) at (40:3);
\coordinate (c) at (0:3);
\coordinate (d) at ({cos(40)*3},0);
\coordinate (e) at ($(c) + (0,{(tan 20)*3})$);
\coordinate (f) at ($(c) + (0,{(tan 40)*3})$);
\draw (a) -- node[above,yshift=.5mm] {$1$} (b);
\draw (a) -- node[below] {$1$} (c);
\begin{scope}[cgreen]
\draw (b) arc (40:0:3);
\node at (20:2.8) {$\phi$};
\end{scope}
\node[anchor=east] at (a) {$A$};
\node[anchor=south,xshift=-1mm] at (b) {$B$};
\node[anchor=north] at (c) {$C$};
\mpause[1]{
\begin{scope}[cred]
\node[anchor=north] at (d) {$D$};
\draw (b) -- node[pos=.65,left] {$\sin \phi$} (d);
\end{scope}
}
\mpause[4]{
\begin{scope}[cblue]
\draw (c) -- (e) -- node[anchor=west,at start] {$E$} (b);
\end{scope}
\begin{scope}[gray]
\draw ($(c) + (-2mm,0)$) -- ++(0,2mm) -- ++(2mm,0);
\draw ($(b) + (-140:2mm)$) -- ++(-50:2mm) -- ++(40:2mm);
\end{scope}
}
\mpause[6]{
\begin{scope}[cblue]
\draw (c) -- (f) -- node[anchor=west,at start] {$F$} (b);
\end{scope}
\begin{scope}[gray]
\draw ($(b) + (-140:-2mm)$) -- ++(-50:2mm) -- ++(40:-2mm);
\end{scope}
}
\mpause[9]{
\begin{scope}[xshift=60mm,yshift=10mm]
\draw (0,0) -- node[below] {$a$} (3,0) -- node[right] {$b$} (3,1.5) -- cycle;
\draw (26:1.2) arc (26:0:1.2);
\node at (13:.9) {$\alpha$};
\mpause[10]{ \node[align=center] at (1.5,-.7) {$\tan \alpha = \frac{b}{a}$}; }
\mpause[11]{ \node[align=center] at (1.5,-1.2) {$b = a \cdot \tan \alpha$}; }
\end{scope}
}
\end{tikzpicture}
\end{center}\vspace{-2ex}
\begin{talign}
&\mpause[2]{\sin \phi = |BD| < \phi}
\mpause[3]{\quad\implies\quad \frac{\sin \phi}{\phi} < 1}
\\
&
\mpause[5]{ \phi < |CE| + |EB| }
\mpause[7]{\;\text{ \& }\; |EB| < |EF|}
\mpause[8]{\quad\implies\quad \phi < |CE| + |EF| = |CF|} \\
&\mpause[12]{\phi < |CF|} \mpause[13]{ = 1\cdot \tan \phi} \mpause[14]{= \frac{\sin \phi}{\cos \phi}}
\mpause[15]{\quad\implies\quad \alert{\cos \phi < \frac{\sin \phi}{\phi} < 1}}
\end{talign}%
\pause[+19]%
We use the Squeeze Theorem:\vspace{-1ex}
\begin{talign}
\lim_{\phi \to 0} \cos \phi = 1 = \lim_{\phi \to 0} 1
&& \mpause[1]{\implies} && \mpause[1]{\alert{\lim_{\phi\to 0}\frac{\sin \phi}{\phi} = 1}}
\end{talign}
\end{frame}

