
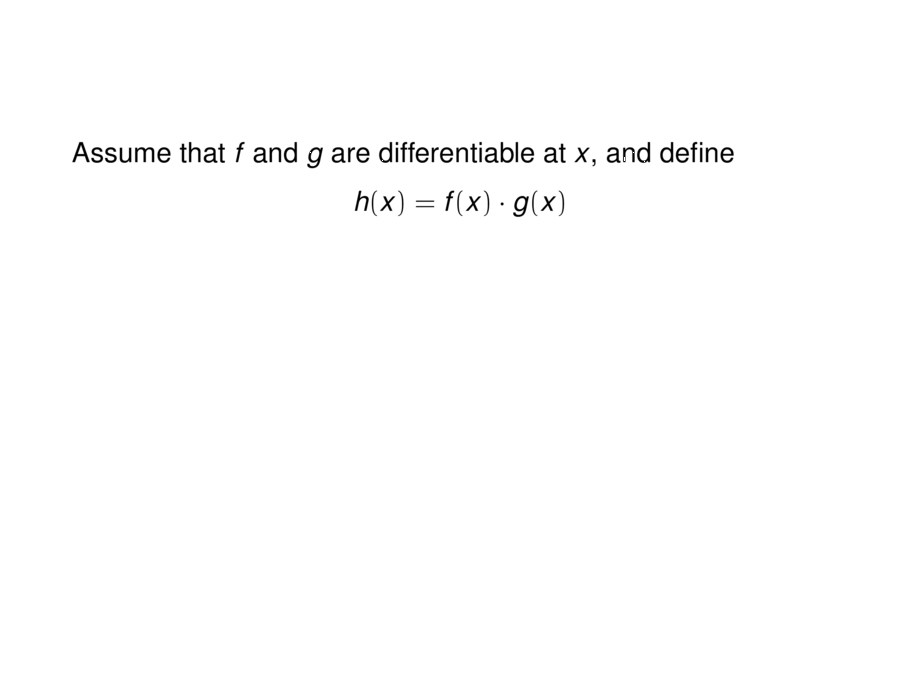


































































































11/155
\begin{frame}
\frametitle{Differentiation Rules: Product Rule}
Assume that $f$ and $g$ are differentiable at $x$, and define
\begin{talign}
h(x) = f(x) \cdot g(x)
\end{talign}
\pause
We try to find the derivative of $h$ at $x$:
\begin{talign}
\begin{aligned}
h'(x) = \lim_{\Delta x \to 0} \frac{\Delta h}{\Delta x}
\end{aligned}
&&\mpause[1]{\text{where}}&&
\mpause[1]{
\begin{aligned}
\Delta h &= h(x+\Delta x) - h(x) \\
\Delta f &= f(x+\Delta x) - f(x) \\
\Delta g &= g(x+\Delta x) - g(x)
\end{aligned}
}
\end{talign}
\pause\pause
Then
\begin{talign}
\Delta h &= \mpause[1]{ f(x+\Delta x)\cdot g(x+\Delta x) - f(x)\cdot g(x) } \\
&\mpause[2]{= (f(x) + \Delta f) \cdot (g(x) + \Delta g) - f(x)\cdot g(x)}\\
&\mpause[3]{= \Delta f\cdot g(x) + f(x) \cdot \Delta g + \Delta f \cdot \Delta g}
\end{talign}
\end{frame}

