


































































































47/81
\begin{frame}
\frametitle{Derivatives of Basic Functions}
\begin{exampleblock}{}
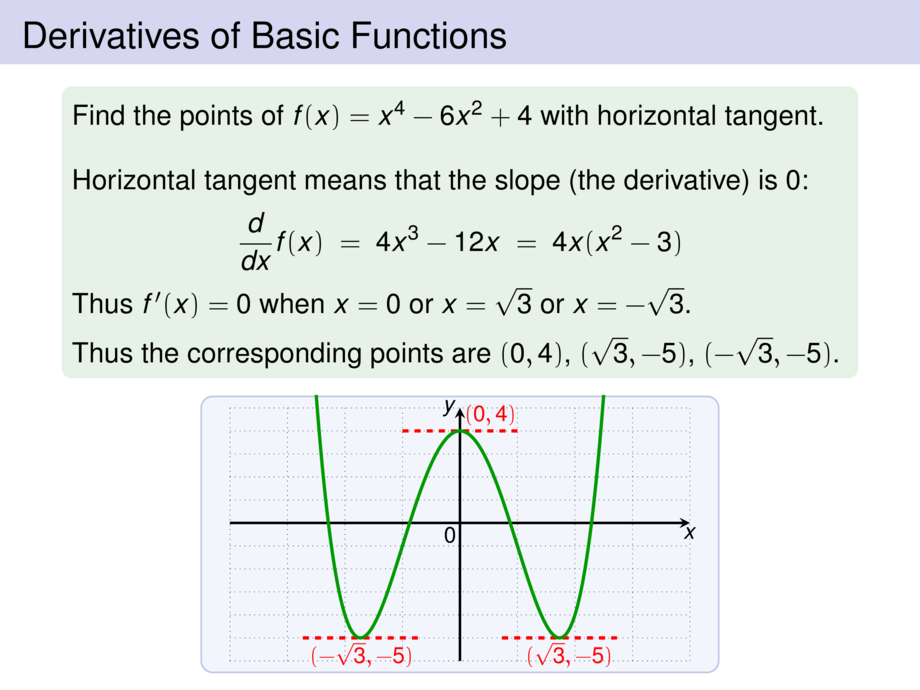
Find the points of $f(x) = x^4 - 6x^2 + 4$ with horizontal tangent.
\pause\bigskip
Horizontal tangent means that the slope (the derivative) is $0$:
\begin{talign}
\frac{d}{dx} f(x) \;=\; \mpause[1]{4x^3 - 12x} \mpause[2]{\;=\; 4x(x^2 - 3)}
\end{talign}
\pause\pause\pause
Thus $f'(x) = 0$ when $x = 0$ or $x = \sqrt{3}$ or $x = -\sqrt{3}$.\pause\medskip
Thus the corresponding points are $(0,4)$, $(\sqrt{3},-5)$, $(-\sqrt{3},-5)$.
\end{exampleblock}
\pause
\begin{center}
\scalebox{.8}{
\begin{tikzpicture}[default,baseline=1cm,yscale=.4]
\diagram{-4}{4}{-6}{5}{1}
\diagramannotatez
\begin{scope}[ultra thick]
\draw[cred,dashed] (-1,4) -- node[above right] {$(0,4)$} (1,4) ;
\draw[cred,dashed] ({-sqrt(3)-1},-5) -- ({-sqrt(3)+1},-5) node[below left] {$(-\sqrt{3},-5)$};
\draw[cred,dashed] ({sqrt(3)-1},-5) -- ({sqrt(3)+1},-5) node[below left] {$(\sqrt{3},-5)$};
\draw[cgreen,ultra thick] plot[smooth,domain=-2.5:2.5,samples=200] function{x**4 - 6*x**2 + 4};
\end{scope}
\end{tikzpicture}
}
\end{center}
\end{frame}

